Hadwiger–Nelson problem

Unsolved problem in mathematics:

How many colors are needed to color the plane so that no two points at unit distance are the same color?

(more unsolved problems in mathematics)

A seven-coloring of the plane, and a four-chromatic unit distance graph in the plane (the Moser spindle), proving that the chromatic number of a plane is bounded above by 7 and below by 4

The Golomb graph, Solomon W. Golomb's ten-vertex four-chromatic unit distance graph

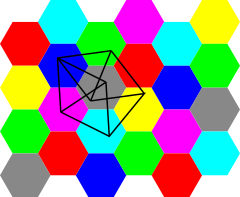
In geometric graph theory, the Hadwiger–Nelson problem, named after Hugo Hadwiger and Edward Nelson, asks for the minimum number of colors required to color the plane such that no two points at distance 1 from each other have the same color. The answer is unknown, but has been narrowed down to one of the numbers 5, 6 or 7. The correct value may depend on the choice of axioms for set theory.

Relation to finite graphs

The question can be phrased in graph theoretic terms as follows. Let G be the unit distance graph of the plane: an infinite graph with all points of the plane as vertices and with an edge between two vertices if and only if the distance between the two points is 1. The Hadwiger–Nelson problem is to find the chromatic number of G. As a consequence, the problem is often called "finding the chromatic number of the plane". By the de Bruijn–Erdős theorem, a result of de Bruijn & Erdős (1951), the problem is equivalent (under the assumption of the axiom of choice) to that of finding the largest possible chromatic number of a finite unit distance graph.

History

According to Jensen & Toft (1995), the problem was first formulated by Nelson in 1950, and first published by Gardner (1960). Hadwiger (1945) had earlier published a related result, showing that any cover of the plane by five congruent closed sets contains a unit distance in one of the sets, and he also mentioned the problem in a later paper (Hadwiger 1961). Soifer (2008) discusses the problem and its history extensively.

One application of the problem connects it to the Beckman–Quarles theorem, according to which any mapping of the Euclidean plane (or any higher dimensional space) to itself that preserves unit distances must be an isometry, preserving all distances. Finite colorings of these spaces can be used to construct mappings from them to higher-dimensional spaces that preserve distances but are not isometries. For instance, the Euclidean plane can be mapped to a six-dimensional space by coloring it with seven colors so that no two points at distance one have the same color, and then mapping the points by their colors to the seven vertices of a six-dimensional regular simplex with unit-length edges. This maps any two points at unit distance to distinct colors, and from there to distinct vertices of the simplex, at unit distance apart from each other. However, it maps all other distances to zero or one, so it is not an isometry. If the number of colors needed to color the plane could be reduced from seven to a lower number, the same reduction would apply to the dimension of the target space in this construction.

Lower and upper bounds

The fact that the chromatic number of the plane must be at least four follows from the existence of a seven-vertex unit distance graph with chromatic number four, named the Moser spindle after its discovery in 1961 by the brothers William and Leo Moser. This graph consists of two unit equilateral triangles joined at a common vertex, x. Each of these triangles is joined along another edge to another equilateral triangle; the vertices y and z of these joined triangles are at unit distance from each other. If the plane could be three-colored, the coloring within the triangles would force y and z to both have the same color as x, but then, since y and z are at unit distance from each other, we would not have a proper coloring of the unit distance graph of the plane. Therefore, at least four colors are needed to color this graph and the plane containing it. An alternative lower bound in the form of a ten-vertex four-chromatic unit distance graph, the Golomb graph, was discovered at around the same time by Solomon W. Golomb.

The lower bound was raised to five in 2018, when computer scientist and biogerontologist Aubrey de Grey found a 1581-vertex, non-4-colourable unit-distance graph. The proof is computer assisted. Mathematician Gil Kalai and computer scientist Scott Aaronson posted discussion of de Grey's finding, with Aaronson reporting independent verifications of de Grey's result using SAT solvers. Kalai linked additional posts by Jordan Ellenberg and Noam Elkies, with Elkies and (separately) de Grey proposing a Polymath project to find non-4-colorable unit distance graphs with fewer vertices than the one in de Grey's construction. As of 2021, the smallest known unit distance graph with chromatic number 5 has 509 vertices. The page of the Polymath project, Polymath (2018), contains further research, media citations and verification data.

The upper bound of seven on the chromatic number follows from the existence of a tessellation of the plane by regular hexagons, with diameter slightly less than one, that can be assigned seven colors in a repeating pattern to form a 7-coloring of the plane. According to Soifer (2008), this upper bound was first observed by John R. Isbell.

Variations

The problem can easily be extended to higher dimensions. Finding the chromatic number of 3-space is a particularly interesting problem. As with the version on the plane, the answer is not known, but has been shown to be at least 6 and at most 15.

In the n-dimensional case of the problem, an easy upper bound on the number of required colorings found from tiling n-dimensional cubes is $\lfloor 2+{\sqrt {n}}\rfloor ^{n}$. A lower bound from simplexes is $n+1$. For $n>1$, a lower bound of $n+2$ is available using a generalization of the Moser spindle: a pair of the objects (each two simplexes glued together on a facet) which are joined on one side by a point and the other side by a line. An exponential lower bound was proved by Frankl and Wilson in 1981.

One can also consider colorings of the plane in which the sets of points of each color are restricted to sets of some particular type. Such restrictions may cause the required number of colors to increase, as they prevent certain colorings from being considered acceptable. For instance, if a coloring of the plane consists of regions bounded by Jordan curves, then at least six colors are required.

See also

• Four color theorem

References

• Aaronson, Scott (April 11, 2018), Amazing progress on longstanding open problems
• Beckman, F. S.; Quarles, D. A. Jr. (1953), "On isometries of Euclidean spaces", Proceedings of the American Mathematical Society, 4 (5): 810–815, doi:10.2307/2032415, JSTOR 2032415, MR 0058193
• de Bruijn, N. G.; Erdős, P. (1951), "A colour problem for infinite graphs and a problem in the theory of relations", Nederl. Akad. Wetensch. Proc. Ser. A, 54: 371–373, CiteSeerX 10.1.1.210.6623, doi:10.1016/S1385-7258(51)50053-7
• Chilakamarri, K. B. (1993), "The unit-distance graph problem: a brief survey and some new results", Bull Inst. Combin. Appl., 8: 39–60
• Chilakamarri, Kiran B.; Mahoney, Carolyn R. (1996), "Unit-distance graphs, graphs on the integer lattice and a Ramsey type result", Aequationes Mathematicae, 51 (1–2): 48–67, doi:10.1007/BF01831139, MR 1372782, S2CID 189831504
• Coulson, D. (2004). "On the chromatic number of plane tilings". Journal of the Australian Mathematical Society. 77 (2). Cambridge University Press (CUP): 191–196. doi:10.1017/s1446788700013574. ISSN 1446-7887.
• Coulson, D. (2002), "A 15-colouring of 3-space omitting distance one", Discrete Math., 256 (1–2): 83–90, doi:10.1016/S0012-365X(01)00183-2
• Croft, Hallard T.; Falconer, Kenneth J.; Guy, Richard K. (1991), Unsolved Problems in Geometry, Springer-Verlag, Problem G10, ISBN 978-0-387-97506-1
• Frankl, P.; Wilson, R.M. (1981), "Intersection theorems with geometric consequences", Combinatorica, 1 (4): 357–368, doi:10.1007/BF02579457, S2CID 6768348
• Gardner, Martin (October 1960), "A new collection of 'brain-teasers'", Mathematical Games, Scientific American, 203 (4): 180, doi:10.1038/scientificamerican1060-218 (inactive 1 November 2024), JSTOR 24940666{{citation}}: CS1 maint: DOI inactive as of November 2024 (link) CS1 maint: date and year (link)
• de Grey, Aubrey D.N.J. (2018), "The Chromatic Number of the Plane Is at least 5", Geombinatorics, 28: 5–18, arXiv:1804.02385, Bibcode:2016arXiv160407134W, MR 3820926
• Hadwiger, Hugo (1945), "Überdeckung des euklidischen Raumes durch kongruente Mengen", Portugal. Math., 4: 238–242
• Hadwiger, Hugo (1961), "Ungelöste Probleme No. 40", Elem. Math., 16: 103–104
• Heule, Marijn J.H. (2018), Computing Small Unit-Distance Graphs with Chromatic Number 5, arXiv:1805.12181, Bibcode:2018arXiv180512181H
• Jensen, Tommy R.; Toft, Bjarne (1995), Graph Coloring Problems, Wiley-Interscience Series in Discrete Mathematics and Optimization, pp. 150–152, ISBN 978-0-471-02865-9
• Kalai, Gil (April 10, 2018), Aubrey de Grey: The chromatic number of the plane is at least 5
• Mixon, Dustin (February 1, 2021), Polymath16, seventeenth thread: Declaring victory, retrieved 16 August 2021
• Polymath, D. H. J. (April 2018), Hadwiger-Nelson problem (Polymath project page), archived from the original on 2022-02-16
• Radoičić, Radoš; Tóth, Géza (2003), "Note on the chromatic number of the space", in Aronov, Boris; Basu, Saugata; Pach, Janos; Sharir, Micha (eds.), Discrete and Computational Geometry: The Goodman–Pollack Festschrift (PDF), Algorithms and Combinatorics, vol. 25, Berlin: Springer, pp. 695–698, doi:10.1007/978-3-642-55566-4_32, ISBN 978-3-540-00371-7, MR 2038498
• Rassias, Themistocles M. (2001), "Isometric mappings and the problem of A. D. Aleksandrov for conservative distances", in Florian, H.; Ortner, N.; Schnitzer, F. J.; Tutschke, W. (eds.), Functional-Analytic and Complex Methods, their Interactions, and Applications to Partial Differential Equations: Proceedings of the International Workshop held at Graz University Of Technology, Graz, February 12–16, 2001, River Edge, New Jersey: World Scientific Publishing Co., Inc., pp. 118–125, doi:10.1142/4822, ISBN 978-981-02-4764-5, MR 1893253
• Shelah, Saharon; Soifer, Alexander (2003), "Axiom of choice and chromatic number of the plane", Journal of Combinatorial Theory, Series A, 103 (2): 387–391, doi:10.1016/S0097-3165(03)00102-X
• Soifer, Alexander (2008), The Mathematical Coloring Book: Mathematics of Coloring and the Colorful Life of its Creators, New York: Springer, ISBN 978-0-387-74640-1
• Woodall, D. R. (1973), "Distances realized by sets covering the plane", Journal of Combinatorial Theory, Series A, 14 (2): 187–200, doi:10.1016/0097-3165(73)90020-4, MR 0310770

External links

• O'Rourke, Joseph, "Problem 57: Chromatic Number of the Plane", The Open Problems Project
• Mohar, Bojan (2001), The chromatic number of the Unit Distance Graph
• Kalai, Gil (2018), Coloring Problems for Arrangements of Circles (and Pseudocircles)
• Grime, James (February 27, 2019), "A Colorful Unsolved Problem", Numberphile, archived from the original on 2021-12-21