Fish curve

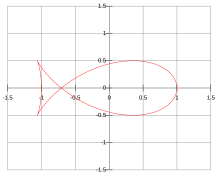The fish curve with scale parameter a = 1

A fish curve is an ellipse negative pedal curve that is shaped like a fish. In a fish curve, the pedal point is at the focus for the special case of the squared eccentricity $e^{2}={\tfrac {1}{2}}$. The parametric equations for a fish curve correspond to those of the associated ellipse.

Equations

For an ellipse with the parametric equations $$\textstyle {x=a\cos(t),\qquad y={\frac {a\sin(t)}{\sqrt {2}}}},$$ the corresponding fish curve has parametric equations $$\textstyle {x=a\cos(t)-{\frac {a\sin ^{2}(t)}{\sqrt {2}}},\qquad y=a\cos(t)\sin(t)}.$$

When the origin is translated to the node (the crossing point), the Cartesian equation can be written as: $$\left(2x^{2}+y^{2}\right)^{2}-2{\sqrt {2}}ax\left(2x^{2}-3y^{2}\right)+2a^{2}\left(y^{2}-x^{2}\right)=0.$$

Properties

Area

The area of a fish curve is given by: $${\begin{aligned}A&={\frac {1}{2}}\left|\int {\left(xy'-yx'\right)dt}\right|\\&={\frac {1}{8}}a^{2}\left|\int {\left[3\cos(t)+\cos(3t)+2{\sqrt {2}}\sin ^{2}(t)\right]dt}\right|,\end{aligned}}$$ so the area of the tail and head are given by: $${\begin{aligned}A_{\text{Tail}}&=\left({\frac {2}{3}}-{\frac {\pi }{4{\sqrt {2}}}}\right)a^{2},\\A_{\text{Head}}&=\left({\frac {2}{3}}+{\frac {\pi }{4{\sqrt {2}}}}\right)a^{2},\end{aligned}}$$ giving the overall area for the fish as: $$A={\frac {4}{3}}a^{2}.$$

Curvature, arc length, and tangential angle

The arc length of the curve is given by $$a{\sqrt {2}}\left({\frac {1}{2}}\pi +3\right).$$

The curvature of a fish curve is given by: $$K(t)={\frac {2{\sqrt {2}}+3\cos(t)-\cos(3t)}{2a\left[\cos ^{4}t+\sin ^{2}t+\sin ^{4}t+{\sqrt {2}}\sin(t)\sin(2t)\right]^{\frac {3}{2}}}},$$ and the tangential angle is given by: $$\phi (t)=\pi -\arg \left({\sqrt {2}}-1-{\frac {2}{\left(1+{\sqrt {2}}\right)e^{it}-1}}\right),$$ where $\arg(z)$ is the complex argument.