Jump to content

File:PartialOrders redundencies.pdf

Page contents not supported in other languages.
This is a file from the Wikimedia Commons
From Wikipedia, the free encyclopedia

PartialOrders_redundencies.pdf (383 × 383 pixels, file size: 52 KB, MIME type: application/pdf)

Summary

Description
English: Connection between strict and non-strict partial orders established by converse (cnv), reflexive closure (cls), and irreflexive kernel (ker). The mappings cls and ker (on the domain of irreflexive and reflexive relations, respectively) are inverse to each other, and cnv is inverse to itself, and commutes with cls and with ker. Therefore, we have a commutative diagram.

For illustration, we use four example relations on the set {1,2,3,4,5}. Each relation table shows a "*" whenever (x,y)∈R holds, where x and y corresponds to the row and column, respectively, like this:

Each of the four relations corresponds, with some (own) grain of salt, to the one Hasse diagram in the image center: Since a Hasse diagram cannot show if an element is related to itself, such relations must be tacitly understood to be absent for the strict versions, and present for the non-strict ones. For the ">" and the "≥" relation, the diagram must be read upside-down.

Moreover, if cpl denotes the complement of a relation, then, for every non-strict partial order R, one has

  1. cnv(ker(R)) ⊆ cpl(R), and
  2. equality holds iff R is a non-strict total order.
Proof of (1): If (x,y) ∈ cnv(ker(R)), then (y,x) ∈ ker(R), hence (y,x) ∈ ker(R) and y≠x, hence (x,y) ∉ R, since else x=y by asymmetry, hence (x,y) ∈ cpl(R).
Proof of (2): "If": Let R be connected, let (x,y) ∈ cpl(R), then (x,y) ∉ R, hence (y,x) ∈ R, which also implies that x≠y, hence (y,x) ∈ ker(R), hence (x,y) ∈ cnv(ker(R)).
"Only if": Assume for contradiction equality for a non-connected partial order R. Let (x,y), (y,x) ∉ R, then (x,y) ∈ cpl(R), hence (x,y) ∈ cnv(ker(R)), hence (y,x) ∈ ker(R), hence (y,x) ∈ R, contradicting the assumption.
Date
Source Own work
Author Jochen Burghardt
Other versions File:PartialOrders redundencies.pdf * File:PartialOrders redundencies svg.svg
LaTeX source code
\documentclass[12pt]{article}
\usepackage[pdftex]{color}
\usepackage{amssymb}
\usepackage[paperwidth=65mm,paperheight=65mm]{geometry}
\setlength{\topmargin}{-36mm}
\setlength{\textwidth}{65mm}
\setlength{\textheight}{65mm}
\setlength{\evensidemargin}{0cm}
\setlength{\oddsidemargin}{-23mm}
\setlength{\parindent}{0cm}
\setlength{\parskip}{1ex}
\setlength{\unitlength}{1mm}
\sloppy
\begin{document}
\renewcommand{\leq}{\leqslant}
\renewcommand{\geq}{\geqslant}

% foreground
\definecolor{fOp}       {rgb}{0.00,0.00,0.50}   % operation
\definecolor{fNm}       {rgb}{0.50,0.50,0.50}   % canonical name
\definecolor{fTb}       {rgb}{0.50,0.50,0.50}   % relation table
\definecolor{fY}        {rgb}{0.00,0.00,0.00}   % related
\definecolor{fN}        {rgb}{0.90,0.90,0.90}   % unrelated
\definecolor{fStr}      {rgb}{0.50,0.00,0.00}   % strict
\definecolor{fNSt}      {rgb}{0.00,0.50,0.00}   % non-strict
\definecolor{fNd}       {rgb}{0.00,0.00,0.75}   % Hasse node
\definecolor{fAr}       {rgb}{0.80,0.80,0.99}   % Hasse arc
% background
\definecolor{bStr}      {rgb}{0.99,0.94,0.94}   % strict
\definecolor{bNSt}      {rgb}{0.94,0.99,0.94}   % non-strict
\definecolor{bHs}       {rgb}{0.99,0.99,0.99}   % Hasse diagram

\renewcommand{\arraystretch}{0.10}
\newcommand{\0}{\textcolor{fN}{*}}
\newcommand{\1}{\textcolor{fY}{*}}
\newcommand{\p}{\0}

\newcommand{\GE}{%      x >= y
        \begin{array}{@{}|@{}c@{}c@{}c@{}c@{}c@{}@{}}%
        \hline%
        \1 & \0 & \0 & \0& \0   \\% 1   <-- x
        \1 & \1 & \0 & \0& \0   \\% 2
        \1 & \1 & \1 & \0& \0   \\% 3
        \1 & \1 & \p & \1& \0   \\% 4
        \1 & \1 & \1 & \1& \1   \\% 5
% y -->  1    2    3    4   5
        %\hline%
        \end{array}%
}

\newcommand{\GT}{%      x > y
        \begin{array}{@{}|@{}c@{}c@{}c@{}c@{}c@{}@{}}%
        \hline%
        \0 & \0 & \0 & \0& \0   \\% 1   <-- x
        \1 & \0 & \0 & \0& \0   \\% 2
        \1 & \1 & \0 & \0& \0   \\% 3
        \1 & \1 & \p & \0& \0   \\% 4
        \1 & \1 & \1 & \1& \0   \\% 5
% y -->  1    2    3    4   5
        %\hline%
        \end{array}%
}

\newcommand{\LE}{%      x <= y
        \begin{array}{@{}|@{}c@{}c@{}c@{}c@{}c@{}@{}}%
        \hline%
        \1 & \1 & \1 & \1& \1   \\% 1   <-- x
        \0 & \1 & \1 & \1& \1   \\% 2
        \0 & \0 & \1 & \p& \1   \\% 3
        \0 & \0 & \0 & \1& \1   \\% 4
        \0 & \0 & \0 & \0& \1   \\% 5
% y -->  1    2    3    4   5
        %\hline%
        \end{array}%
}

\newcommand{\LT}{%      x < y
        \begin{array}{@{}|@{}c@{}c@{}c@{}c@{}c@{}@{}}%
        \hline%
        \0 & \1 & \1 & \1& \1   \\% 1   <-- x
        \0 & \0 & \1 & \1& \1   \\% 2
        \0 & \0 & \0 & \p& \1   \\% 3
        \0 & \0 & \0 & \0& \1   \\% 4
        \0 & \0 & \0 & \0& \0   \\% 5
% y -->  1    2    3    4   5
        %\hline%
        \end{array}%
}

\begin{picture}(60,60)
\thicklines
\textcolor{bStr}{\put(30,30){\makebox(0,0)[b]{\rule{60mm}{30mm}}}}%
\textcolor{bNSt}{\put(30,30){\makebox(0,0)[t]{\rule{60mm}{30mm}}}}%
\textcolor{fStr}{\put(30,59){\makebox(0,0)[t]{strict}}}%
\textcolor{fNSt}{\put(30, 1){\makebox(0,0)[b]{non-strict}}}%
\textcolor{fTb}{\put(10,10){\makebox(0,0){$\LE$}}}%
\textcolor{fTb}{\put(10,50){\makebox(0,0){$\LT$}}}%
\textcolor{fTb}{\put(50,10){\makebox(0,0){$\GE$}}}%
\textcolor{fTb}{\put(50,50){\makebox(0,0){$\GT$}}}%
\textcolor{fNm}{\put( 3, 4){\makebox(0,0)[t]{$\leq$}}}%
\textcolor{fNm}{\put( 3,56){\makebox(0,0)[b]{$<$}}}%
\textcolor{fNm}{\put(57, 4){\makebox(0,0)[t]{$\geq$}}}%
\textcolor{fNm}{\put(57,56){\makebox(0,0)[b]{$>$}}}%
\textcolor{fOp}{\put(17,11){\vector(1,0){26}}}%
\textcolor{fOp}{\put(30,12){\makebox(0,0)[b]{$\it cnv$}}}%
\textcolor{fOp}{\put(43,9){\vector(-1,0){26}}}%
\textcolor{fOp}{\put(30,8){\makebox(0,0)[t]{$\it cnv$}}}%
\textcolor{fOp}{\put(17,51){\vector(1,0){26}}}%
\textcolor{fOp}{\put(30,52){\makebox(0,0)[b]{$\it cnv$}}}%
\textcolor{fOp}{\put(43,49){\vector(-1,0){26}}}%
\textcolor{fOp}{\put(30,48){\makebox(0,0)[t]{$\it cnv$}}}%
\textcolor{fOp}{\put(11,17){\vector(0,1){26}}}%
\textcolor{fOp}{\put(12,30){\makebox(0,0)[l]{$\it ker$}}}%
\textcolor{fOp}{\put( 9,43){\vector(0,-1){26}}}%
\textcolor{fOp}{\put( 8,30){\makebox(0,0)[r]{$\it cls$}}}%
\textcolor{fOp}{\put(51,17){\vector(0,1){26}}}%
\textcolor{fOp}{\put(52,30){\makebox(0,0)[l]{$\it ker$}}}%
\textcolor{fOp}{\put(49,43){\vector(0,-1){26}}}%
\textcolor{fOp}{\put(48,30){\makebox(0,0)[r]{$\it cls$}}}%
%
\textcolor{bHs}{\put(25,23){\makebox(0,0)[bl]{\rule{10mm}{14mm}}}}%
\thinlines
\textcolor{fAr}{\put(30,24){\line(0,1){4}}}%
\textcolor{fAr}{\put(30,28){\line(-1,1){4}}}%
\textcolor{fAr}{\put(30,28){\line(1,1){4}}}%
\textcolor{fAr}{\put(26,32){\line(1,1){4}}}%
\textcolor{fAr}{\put(34,32){\line(-1,1){4}}}%
\textcolor{bHs}{\put(30,24){\makebox(0,0){\rule{2mm}{2mm}}}}%
\textcolor{bHs}{\put(30,28){\makebox(0,0){\rule{2mm}{2mm}}}}%
\textcolor{bHs}{\put(26,32){\makebox(0,0){\rule{2mm}{2mm}}}}%
\textcolor{bHs}{\put(34,32){\makebox(0,0){\rule{2mm}{2mm}}}}%
\textcolor{bHs}{\put(30,36){\makebox(0,0){\rule{2mm}{2mm}}}}%
\textcolor{fNd}{\put(30,24){\makebox(0,0){$\scriptscriptstyle 1$}}}%
\textcolor{fNd}{\put(30,28){\makebox(0,0){$\scriptscriptstyle 2$}}}%
\textcolor{fNd}{\put(26,32){\makebox(0,0){$\scriptscriptstyle 3$}}}%
\textcolor{fNd}{\put(34,32){\makebox(0,0){$\scriptscriptstyle 4$}}}%
\textcolor{fNd}{\put(30,36){\makebox(0,0){$\scriptscriptstyle 5$}}}%
\end{picture}
\end{document}

Licensing

I, the copyright holder of this work, hereby publish it under the following license:
w:en:Creative Commons
attribution share alike
This file is licensed under the Creative Commons Attribution-Share Alike 4.0 International license.
You are free:
  • to share – to copy, distribute and transmit the work
  • to remix – to adapt the work
Under the following conditions:
  • attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
  • share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.

Captions

Add a one-line explanation of what this file represents

Items portrayed in this file

depicts

inception

29 July 2021

media type

application/pdf

File history

Click on a date/time to view the file as it appeared at that time.

Date/TimeThumbnailDimensionsUserComment
current09:54, 1 January 2022Thumbnail for version as of 09:54, 1 January 2022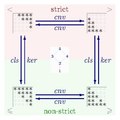383 × 383 (52 KB)Jochen Burghardtmirror row/col in image
15:25, 31 July 2021Thumbnail for version as of 15:25, 31 July 2021383 × 383 (52 KB)Jochen Burghardtused *partial* order example, added hasse diagram, colorized strict/nonstrict
19:18, 29 July 2021Thumbnail for version as of 19:18, 29 July 2021383 × 383 (41 KB)Jochen BurghardtUploaded own work with UploadWizard
No pages on the English Wikipedia use this file (pages on other projects are not listed).

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.

If the file has been modified from its original state, some details may not fully reflect the modified file.

Retrieved from "https://en.wikipedia.org/wiki/File:PartialOrders_redundencies.pdf"