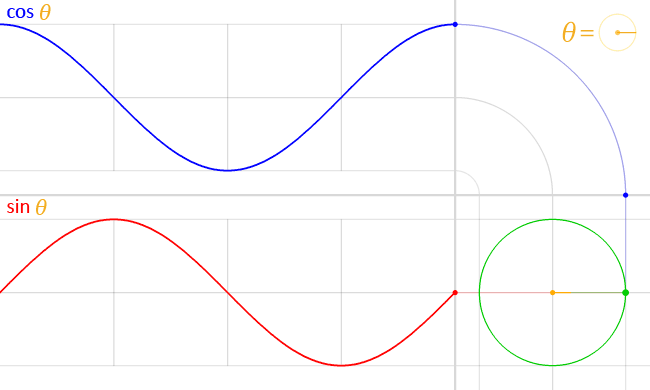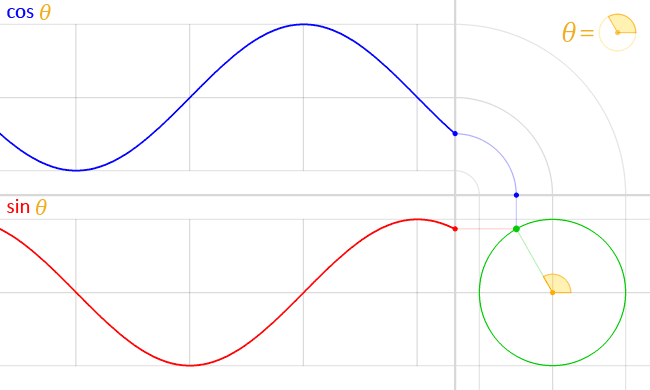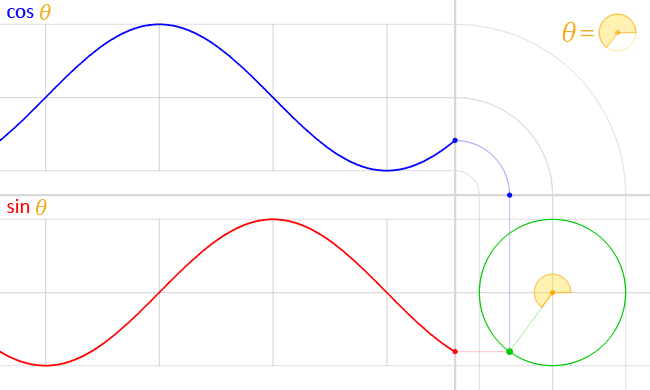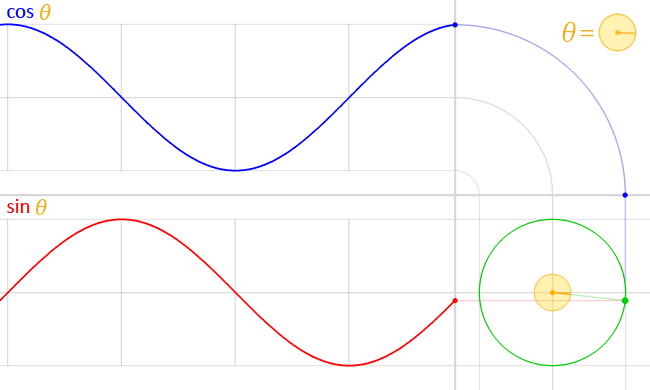
File:Circle cos sin.gif
Appearance
Circle_cos_sin.gif (650 × 390 pixels, file size: 517 KB, MIME type: image/gif, looped, 60 frames, 6.0 s)
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 00:32, 24 June 2014 |  | 650 × 390 (517 KB) | LucasVB | Reverted to version as of 15:59, 16 March 2014 |
| 23:00, 22 June 2014 | 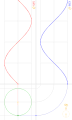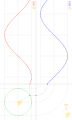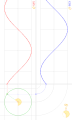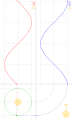 | 390 × 650 (390 KB) | SteinsplitterBot | Bot: Image rotated by 90° | |
| 15:59, 16 March 2014 |  | 650 × 390 (517 KB) | LucasVB | {{Information |Description ={{en|1=sin & cos}} |Source ={{own}} |Author =LucasVB |Date =2014-03-16 |Permission ={{PD-self}} |other_versions = }} Category:Trigonometry [[Category:Trigonometric funct... |
File usage
The following 7 pages use this file:
Global file usage
The following other wikis use this file:
- Usage on ar.wikipedia.org
- Usage on beta.wikiversity.org
- Usage on bn.wikipedia.org
- Usage on ca.wikipedia.org
- Usage on cs.wikipedia.org
- Usage on de.wikipedia.org
- Usage on en.wikibooks.org
- Usage on eu.wikipedia.org
- Usage on fr.wikipedia.org
- Usage on id.wikipedia.org
- Usage on it.wikiversity.org
- Usage on ja.wikipedia.org
- Usage on ja.wikibooks.org
- Usage on ko.wikipedia.org
- Usage on nl.wikipedia.org
- Usage on ru.wikipedia.org
- Usage on ru.wiktionary.org
- Usage on shi.wikipedia.org
- Usage on tr.wikipedia.org
- Usage on uk.wikipedia.org
- Usage on yi.wikipedia.org
- Usage on zh-yue.wikipedia.org