Draft:Interference graph
| Submission declined on 15 September 2024 by Kvng (talk). The proposed article does not have sufficient content to require an article of its own, but it could be merged into the existing article at Register allocation. Since anyone can edit Wikipedia, you are welcome to add that information yourself. Thank you.
Where to get help
How to improve a draft
You can also browse Wikipedia:Featured articles and Wikipedia:Good articles to find examples of Wikipedia's best writing on topics similar to your proposed article. Improving your odds of a speedy review To improve your odds of a faster review, tag your draft with relevant WikiProject tags using the button below. This will let reviewers know a new draft has been submitted in their area of interest. For instance, if you wrote about a female astronomer, you would want to add the Biography, Astronomy, and Women scientists tags. Editor resources
|  |
Comment: Interference graph is a general technique usable for problems other than register allocation. Rather than accepting this as Interference graph (compiler construction) or somesuch as a solution, I think it would be better to improve the existing article on the problem being solved. ~Kvng (talk) 22:43, 15 September 2024 (UTC)
 | This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|
An interference graph is an algorithm used in compiler construction that helps assign local variables to processor registers for a given instruction set architecture (ISA). It is based on the general concept known as "liveness analysis", in which the code is examined to determine which variables are "live" at any given time.
Description
[edit]In most compiled languages, like C or Java, code is organized into blocks that perform a given function. Temporary calculations and values are stored in local variables, normally with no limit imposed on the number or their type. Blocks also optionally pass information back out of the code, the results of their internal calculations, as well as take in information from other blocks, their parameters.[1]
Internally, central processing units (CPUs) attempt to hold these temporary values in processor registers wherever possible. These are the fastest types of computer memory to access and the overall performance of the program is strongly affected by register use. General purpose registers are generally limited to a small number, often 16 or 32 in modern processors, and even fewer in older designs like x86. As a number of these registers serve other purposes, like passing parameters or holding internal state like the stack pointer or program counter,[2] these are a limited resource, and it may not be possible to hold all local variables in registers. Those that cannot are said to spill.[3]
The goal of the interference graph is to examine local variable usage in the code and map their usage over time such that more than one variable can be stored in a single register as they are used at different points in the code.[4] For instance, consider this pseudo-code that performs an increment:[5]
1. a := 0 2. L1: b := a+1 3. c := c+b 4. a := b*2 5. if a<10 goto L1 6. return c
In this example, there are three local variables, a, b and C. However, only two of these are "active" at the same time, as b is produced by a, and then a is produced by b. At no point in this code are the values of a and b needed in a single calculation. This means that a and b can both be assigned to the same processor register.[5]
These usage patterns can become quite difficult to understand. Consider a more complex code example:[6]
1. v := 1 2. z := v+1 3. x := z * v 4. y := x * 2 5. w := x+z * y 6. u := z+2 7. v := u+w+y 8. return v * u
In this example, the value of x on line 3 is constructed from v and z, and z is constructed from v. Therefore, in line 3, only two different values are active, z and v. x is used to calculate the value y on line 4, and then to calculate w on line 5, and is not used after that point. Thus, x is live only for three lines, during which time the values of y and z are also being used. The value v is no longer used at this point and does not appear elsewhere in the program.[6]
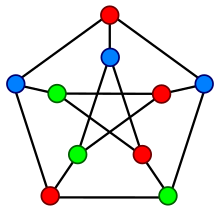
The interference graph provides a way to store the question of which values are active at any given time and thus should be stored in registers if possible. This is accomplished by constructing a graph with the variables as the nodes and the edges connecting nodes that are active at the same time.[7] So for the x node, it has edges to y and z. It does not have a line to v, as x is not yet assigned on line 2, and is not live.[6]
The interference graph does not solve the register allocation by itself, it simply provides a framework to store the information. Assigning the values to registers is typically performed using Chaitin's algorithm, which uses graph coloring to assign a "color" to each of the nodes such that no directly connected nodes have the same color.[8]
References
[edit]Citations
[edit]- ^ Chattopadhyay 2022, p. 144.
- ^ Chattopadhyay 2022, pp. 148–149.
- ^ Austin, p. 12.1.
- ^ Campanoni.
- ^ a b Fegaras, p. 2.
- ^ a b c Fegaras, p. 10.
- ^ Chattopadhyay 2022, p. 150.
- ^ Muchnick 1997, p. 494.
Bibliography
[edit]- Fegaras, Leonidas. "Register Allocation Using the Interference Graph" (PDF). University of Texas, Arlington.
- "Register Allocation Using the Interference Graph". 2014.
- Campanoni, Simone. "Compiler construction: Interference graph" (PDF). Northwestern University.
- Hack, Sebastian (2005). "Interference Graphs of Programs in SSA-form" (PDF). Universit ̈at Karlsruhe.
- Muchnick, Steven (1997). Advanced Compiler Design Implementation. Morgan Kaufmann. pp. 485–499.
- Chattopadhyay, Santanu (2022). "Register Interference Graph Construction". Compiler Design. PHI Learning. pp. 148–155. ISBN 978-93-91818-76-0.
 | This page needs additional or more specific categories. (December 2023) |