Diamond graph
| Diamond graph | |
|---|---|
 | |
| Vertices | 4 |
| Edges | 5 |
| Radius | 1 |
| Diameter | 2 |
| Girth | 3 |
| Automorphisms | 4 (Klein four-group: |
| Chromatic number | 3 |
| Chromatic index | 3 |
| Properties | Hamiltonian Planar Unit distance |
| Table of graphs and parameters | |
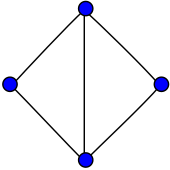
In the mathematical field of graph theory, the diamond graph is a planar, undirected graph with 4 vertices and 5 edges.[1][2] It consists of a complete graph minus one edge.
The diamond graph has radius 1, diameter 2, girth 3, chromatic number 3 and chromatic index 3. It is also a 2-vertex-connected and a 2-edge-connected, graceful,[3] Hamiltonian graph.
Diamond-free graphs and forbidden minor
[edit]A graph is diamond-free if it has no diamond as an induced subgraph. The triangle-free graphs are diamond-free graphs, since every diamond contains a triangle. The diamond-free graphs are locally clustered: that is, they are the graphs in which every neighborhood is a cluster graph. Alternatively, a graph is diamond-free if and only if every pair of maximal cliques in the graph shares at most one vertex.
The family of graphs in which each connected component is a cactus graph is downwardly closed under graph minor operations. This graph family may be characterized by a single forbidden minor. This minor is the diamond graph.[4]
If both the butterfly graph and the diamond graph are forbidden minors, the family of graphs obtained is the family of pseudoforests.
Algebraic properties
[edit]The full automorphism group of the diamond graph is a group of order 4 isomorphic to the Klein four-group, the direct product of the cyclic group with itself.
The characteristic polynomial of the diamond graph is . It is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.
See also
[edit]References
[edit]- ^ Weisstein, Eric W. "Diamond Graph". MathWorld.
- ^ ISGCI: Information System on Graph Classes and their Inclusions "List of Small Graphs".
- ^ Sin-Min Lee, Y.C. Pan and Ming-Chen Tsai. "On Vertex-graceful (p,p+l)-Graphs". [1] Archived 2008-08-07 at the Wayback Machine
- ^ El-Mallah, Ehab; Colbourn, Charles J. (1988), "The complexity of some edge deletion problems", IEEE Transactions on Circuits and Systems, 35 (3): 354–362, doi:10.1109/31.1748.




