Dürer graph

In the mathematical field of graph theory, the Dürer graph is an undirected graph with 12 vertices and 18 edges. It is named after Albrecht Dürer, whose 1514 engraving Melencolia I includes a depiction of Dürer's solid, a convex polyhedron having the Dürer graph as its skeleton. Dürer's solid is one of only four well-covered simple convex polyhedra.
Dürer's solid
[edit]Dürer's solid is combinatorially equivalent to a cube with two opposite vertices truncated,[1] although Dürer's depiction of it is not in this form but rather as a truncated rhombohedron or truncated triangular trapezohedron.[2] The exact geometry of the solid depicted by Dürer is a subject of some academic debate, with different hypothetical values for its acute angles ranging from 72° to 82°.[3]
Graph-theoretic properties
[edit]| Dürer graph | |
|---|---|
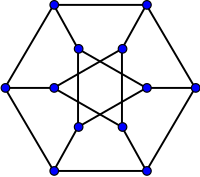 The Dürer graph | |
| Named after | Albrecht Dürer |
| Vertices | 12 |
| Edges | 18 |
| Radius | 3 |
| Diameter | 4 |
| Girth | 3 |
| Automorphisms | 12 (D6) |
| Chromatic number | 3 |
| Chromatic index | 3 |
| Properties | Cubic Planar Well-covered |
| Table of graphs and parameters | |
The Dürer graph is the graph formed by the vertices and edges of the Dürer solid. It is a cubic graph of girth 3 and diameter 4. As well as its construction as the skeleton of Dürer's solid, it can be obtained by applying a Y-Δ transform to the opposite vertices of a cube graph, or as the generalized Petersen graph G(6,2).[4] As with any graph of a convex polyhedron, the Dürer graph is a 3-vertex-connected simple planar graph.
The Dürer graph is a well-covered graph, meaning that all of its maximal independent sets have the same number of vertices, four. It is one of four well-covered cubic polyhedral graphs and one of seven well-covered 3-connected cubic graphs. The only other three well-covered simple convex polyhedra are the tetrahedron, triangular prism, and pentagonal prism.[5]
The Dürer graph is Hamiltonian, with LCF notation [-4,5,2,-4,-2,5;-].[6] More precisely, it has exactly six Hamiltonian cycles, each pair of which may be mapped into each other by a symmetry of the graph.[7]
Symmetries
[edit]The automorphism group both of the Dürer graph and of the Dürer solid (in either the truncated cube form or the form shown by Dürer) is isomorphic to the dihedral group of order 12, denoted D6.
Gallery
[edit]-
The chromatic index of the Dürer graph is 3.
-
The chromatic number of the Dürer graph is 3.
-
The Dürer graph is Hamiltonian.
Notes
[edit]- ^ Weisstein, Eric W., "Dürer's Solid", MathWorld
- ^ Weber (1900).
- ^ Weitzel (2004).
- ^ Pisanski & Tucker (2002).
- ^ Campbell & Plummer (1988); Campbell, Ellingham & Royle (1993).
- ^ Castagna & Prins (1972) attribute the proof of Hamiltonicity of a class of generalized Petersen graphs that includes the Dürer graph to a 1968 Ph.D. thesis of G. N. Robertson at the University of Waterloo.
- ^ Schwenk (1989).
References
[edit]- Campbell, S. R.; Ellingham, M. N.; Royle, Gordon F. (1993), "A characterisation of well-covered cubic graphs", Journal of Combinatorial Mathematics and Combinatorial Computing, 13: 193–212, MR 1220613.
- Campbell, Stephen R.; Plummer, Michael D. (1988), "On well-covered 3-polytopes", Ars Combinatoria, 25 (A): 215–242, MR 0942505.
- Castagna, Frank; Prins, Geert (1972), "Every Generalized Petersen Graph has a Tait Coloring", Pacific Journal of Mathematics, 40: 53–58, doi:10.2140/pjm.1972.40.53.
- Pisanski, Tomaž; Tucker, Thomas W. (2002), "Growth in products of graphs" (PDF), The Australasian Journal of Combinatorics, 26: 155–169, MR 1918150
- Schwenk, Allen J. (1989), "Enumeration of Hamiltonian cycles in certain generalized Petersen graphs", Journal of Combinatorial Theory, Series B, 47 (1): 53–59, doi:10.1016/0095-8956(89)90064-6, MR 1007713.
- Weber, P. (1900), Beiträge zu Dürers Weltanschauung—Eine Studie über die drei Stiche Ritter, Tod und Teufel, Melancholie und Hieronymus im Gehäus, Strassburg
{{citation}}: CS1 maint: location missing publisher (link). As cited by Weitzel (2004). - Weitzel, Hans (2004), "A further hypothesis on the polyhedron of A. Dürer's engraving Melencolia I", Historia Mathematica, 31 (1): 11–14, doi:10.1016/S0315-0860(03)00029-6.



