Compound of twelve pentagrammic prisms
Appearance
| Compound of twelve pentagrammic prisms | |
|---|---|
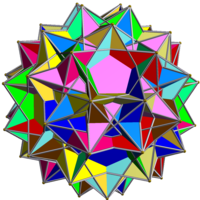
| |
| Type | Uniform compound |
| Index | UC37 |
| Polyhedra | 12 pentagrammic prisms |
| Faces | 24 pentagrams, 60 squares |
| Edges | 180 |
| Vertices | 60 |
| Symmetry group | icosahedral (Ih) |
| Subgroup restricting to one constituent | 5-fold dihedral (D5) |
This uniform polyhedron compound is a symmetric arrangement of 12 pentagrammic prisms, aligned in pairs with the axes of fivefold rotational symmetry of a dodecahedron.
It results from composing the two enantiomorphs of the compound of six pentagrammic prisms. In doing so, the vertices of the two enantiomorphs coincide, with the result that the full compound has two pentagrammic prisms incident on each of its vertices.
Related polyhedra
[edit]This compound shares its vertex arrangement with four uniform polyhedra as follows:
 Rhombicosidodecahedron |
 Small dodecicosidodecahedron |
 Small rhombidodecahedron |
 Small stellated truncated dodecahedron |
 Compound of six pentagrammic prisms |
 Compound of twelve pentagrammic prisms |
References
[edit]- Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79 (3): 447–457, Bibcode:1976MPCPS..79..447S, doi:10.1017/S0305004100052440, MR 0397554, S2CID 123279687.
