Compound of four octahedra with rotational freedom

Compound of four octahedra with rotational freedom
Type	Uniform compound
Index	UC10
Polyhedra	4 octahedra
Faces	8+24 triangles
Edges	48
Vertices	24
Symmetry group	pyritohedral (Th)
Subgroup restricting to one constituent	6-fold improper rotation (S6)

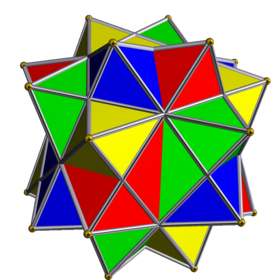
The compound of four octahedra with rotational freedom is a uniform polyhedron compound. It consists in a symmetric arrangement of 4 octahedra, considered as triangular antiprisms. It can be constructed by superimposing four identical octahedra, and then rotating each by an equal angle θ about a separate axis passing through the centres of two opposite octahedral faces, in such a way as to preserve pyritohedral symmetry.

Superimposing this compound with a second copy, in which the octahedra have been rotated by the same angle θ in the opposite direction, yields the compound of eight octahedra with rotational freedom.

When θ = 0, all four octahedra coincide. When θ is 60 degrees, the more symmetric compound of four octahedra (without rotational freedom) arises. In another notable case (pictured), when

$\theta =2\tan ^{-1}\left({\sqrt {15}}-2{\sqrt {3}}\right)\approx 44.47751^{\circ },$

24 of the triangles form coplanar pairs, and the compound assumes the form of the compound of five octahedra with one of the octahedra removed.

Gallery

• Compounds of four octahedra with rotational freedom
• 
  θ = 0°
• 
  θ = 5°
• 
  θ = 10°
• 
  θ = 15°
• 
  θ = 20°
• 
  θ = 25°
• 
  θ = 30°
• 
  θ = 35°
• 
  θ = 40°
• 
  θ = 45°
• 
  θ = 50°
• 
  θ = 55°
• 
  θ = 60°

References

• Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79 (3): 447–457, doi:10.1017/S0305004100052440, MR 0397554.