Circular triangle

Circular triangles with a mixture of convex and concave edges

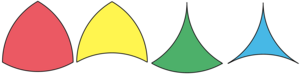
In geometry, a circular triangle is a triangle with circular arc edges.

Examples

Intersection of three disks

Circular horn triangle

Reuleaux triangle

Arbelos

The intersection of three circular disks forms a convex circular triangle. For instance, a Reuleaux triangle is a special case of this construction where the three disks are centered on the vertices of an equilateral triangle, with radius equal to the side length of the triangle. However, not every convex circular triangle is formed as an intersection of disks in this way.

A circular horn triangle has all internal angles equal to zero. One way of forming some of these triangles is to place three circles, externally tangent to each other in pairs; then the central triangular region surrounded by these circles is a horn triangle. However, other horn triangles, such as the arbelos (with three collinear vertices and three semicircles as its sides) are interior to one of the three tangent circles that form it, rather than exterior to all three.

Boscovich's cardioid and one of its perimeter-bisecting lines

A cardioid-like circular triangle found by Roger Joseph Boscovich has three vertices equally spaced on a line, two equal semicircles on one side of the line, and a third semicircle of twice the radius on the other side of the line. The two outer vertices have the interior angle $\pi$ and the middle vertex has interior angle $2\pi$. It has the curious property that all lines through the middle vertex bisect its perimeter.

Other circular triangles can have a mixture of convex and concave circular arc edges.

Characterization of angles

Three given angles $\theta _{1}$, $\theta _{2}$, and $\theta _{3}$ in the interval $[0,2\pi ]$ form the interior angles of a circular triangle (without self-intersections) if and only if they obey the system of inequalities $${\begin{aligned}-2\pi &<\theta _{1}+\theta _{2}-\theta _{3}<2\pi \\-2\pi &<\theta _{1}+\theta _{3}-\theta _{2}<2\pi \\-2\pi &<\theta _{2}+\theta _{3}-\theta _{1}<2\pi .\end{aligned}}$$ All circular triangles with the same interior angles as each other are equivalent to each other under Möbius transformations.

Isoperimetry

Circular triangles give the solution to an isoperimetric problem in which one seeks a curve of minimum length that encloses three given points and has a prescribed area. When the area is at least as large as the circumcircle of the points, the solution is any circle of that area surrounding the points. For smaller areas, the optimal curve will be a circular triangle with the three points as its vertices, and with circular arcs of equal radii as its sides, down to the area at which one of the three interior angles of such a triangle reaches zero. Below that area, the curve degenerates to a circular triangle with "antennae", straight segments reaching from its vertices to one or more of the specified points. In the limit as the area goes to zero, the circular triangle shrinks towards the Fermat point of the given three points.

See also

• Hart circle, a circle associated with certain circular triangles
• Hyperbolic triangle, a triangle that has straight sides in hyperbolic geometry, but is drawn as circular in some models of hyperbolic geometry
• Lune and Lens, two-sided figures bounded by circular arcs
• Sine-triple-angle circle
• Trefoil, a circular triangle bulging outward from its three vertices, used in architecture