Barnette–Bosák–Lederberg graph
| Barnette–Bosák–Lederberg graph | |
|---|---|
 | |
| Vertices | 38 |
| Edges | 57 |
| Radius | 5 |
| Diameter | 9 |
| Girth | 4 |
| Chromatic number | 3 |
| Chromatic index | 3 |
| Properties | Cubic Planar Polyhedral |
| Table of graphs and parameters | |
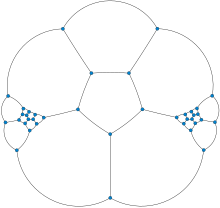
In the mathematical field of graph theory, the Barnette–Bosák–Lederberg graph is a cubic (that is, 3-regular) polyhedral graph with no Hamiltonian cycle, the smallest such graph possible.[1] It was discovered in the mid-1960s by Joshua Lederberg, David Barnette, and Juraj Bosák, after whom it is named. It has 38 vertices and 57 edges.[2][3][4]
Other larger non-Hamiltonian cubic polyhedral graphs include the 46-vertex Tutte graph and a 44-vertex graph found by Emanuels Grīnbergs using Grinberg's theorem. The Barnette–Bosák–Lederberg graph has a similar construction to the Tutte graph but is composed of two Tutte fragments, connected through a pentagonal prism, instead of three connected through a tetrahedron. Without the constraint of having exactly three edges at every vertex, much smaller non-Hamiltonian polyhedral graphs are possible, including the Goldner–Harary graph and the Herschel graph.
References
[edit]- ^ Holton, D. A.; McKay, B. D. (1988), "The smallest non-Hamiltonian 3-connected cubic planar graphs have 38 vertices", Journal of Combinatorial Theory, Series B, 45 (3): 305–319, doi:10.1016/0095-8956(88)90075-5
- ^ Lederberg, Joshua (1967), "Hamilton circuits of convex trivalent polyhedra (up to 18 vertices)", The American Mathematical Monthly, 74 (5): 522–527, doi:10.2307/2314879, JSTOR 2314879, MR 0211895
- ^ Bosák, J. (1967), "Hamiltonian lines in cubic graphs", Theory of Graphs (Internat. Sympos., Rome, 1966), New York: Gordon and Breach, pp. 35–46, MR 0221970
- ^ Weisstein, Eric W., "Barnette-Bosák-Lederberg Graph", MathWorld
