B5 polytope
Appearance
 5-cube |
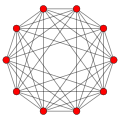 5-orthoplex |
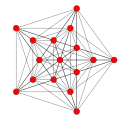 5-demicube |
In 5-dimensional geometry, there are 31 uniform polytopes with B5 symmetry. There are two regular forms, the 5-orthoplex, and 5-cube with 10 and 32 vertices respectively. The 5-demicube is added as an alternation of the 5-cube.
They can be visualized as symmetric orthographic projections in Coxeter planes of the B5 Coxeter group, and other subgroups.
Graphs
[edit]Symmetric orthographic projections of these 32 polytopes can be made in the B5, B4, B3, B2, A3, Coxeter planes. Ak has [k+1] symmetry, and Bk has [2k] symmetry.
These 32 polytopes are each shown in these 5 symmetry planes, with vertices and edges drawn, and vertices colored by the number of overlapping vertices in each projective position.
| # | Graph B5 / A4 [10] |
Graph B4 / D5 [8] |
Graph B3 / A2 [6] |
Graph B2 [4] |
Graph A3 [4] |
Coxeter-Dynkin diagram and Schläfli symbol Johnson and Bowers names |
|---|---|---|---|---|---|---|
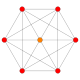
| 1 |  |
 |
 |
 |
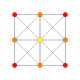
|
h{4,3,3,3} 5-demicube Hemipenteract (hin) |
| 2 |  |
 |
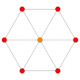 |
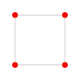 |
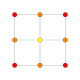
|
{4,3,3,3} 5-cube Penteract (pent) |
| 3 |  |
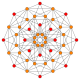 |
 |
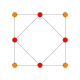 |
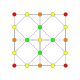
|
t1{4,3,3,3} = r{4,3,3,3} Rectified 5-cube Rectified penteract (rin) |
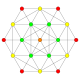
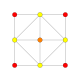
| 4 |  |
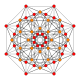 |
 |
 |

|
t2{4,3,3,3} = 2r{4,3,3,3} Birectified 5-cube Penteractitriacontiditeron (nit) |
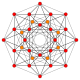
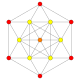
| 5 |  |
 |
 |
 |

|
t1{3,3,3,4} = r{3,3,3,4} Rectified 5-orthoplex Rectified triacontiditeron (rat) |
| 6 |  |
 |
 |
 |

|
{3,3,3,4} 5-orthoplex Triacontiditeron (tac) |
| 7 |  |
 |
 |
 |

|
t0,1{4,3,3,3} = t{3,3,3,4} Truncated 5-cube Truncated penteract (tan) |
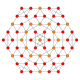
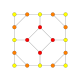
| 8 |  |
 |
 |
 |

|
t1,2{4,3,3,3} = 2t{4,3,3,3} Bitruncated 5-cube Bitruncated penteract (bittin) |
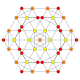
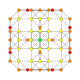
| 9 |  |
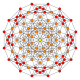 |
 |
 |
|
t0,2{4,3,3,3} = rr{4,3,3,3} Cantellated 5-cube Rhombated penteract (sirn) |
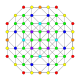
| 10 |  |
 |
 |
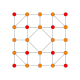 |
|
t1,3{4,3,3,3} = 2rr{4,3,3,3} Bicantellated 5-cube Small birhombi-penteractitriacontiditeron (sibrant) |
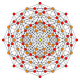
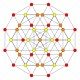
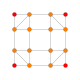
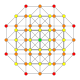
| 11 | 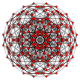 |
 |
 |
 |
|
t0,3{4,3,3,3} Runcinated 5-cube Prismated penteract (span) |
| 12 |  |
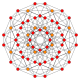 |
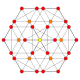 |
 |
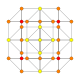
|
t0,4{4,3,3,3} = 2r2r{4,3,3,3} Stericated 5-cube Small celli-penteractitriacontiditeron (scant) |
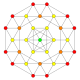
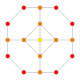
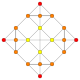
| 13 |  |
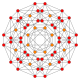 |
 |
 |
|
t0,1{3,3,3,4} = t{3,3,3,4} Truncated 5-orthoplex Truncated triacontiditeron (tot) |
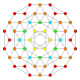
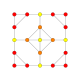
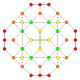
| 14 |  |
 |
 |
 |
|
t1,2{3,3,3,4} = 2t{3,3,3,4} Bitruncated 5-orthoplex Bitruncated triacontiditeron (bittit) |
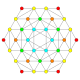
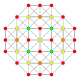
| 15 |  |
 |
 |
 |
|
t0,2{3,3,3,4} = rr{3,3,3,4} Cantellated 5-orthoplex Small rhombated triacontiditeron (sart) |
| 16 |  |
 |
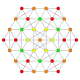 |
 |
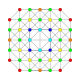
|
t0,3{3,3,3,4} Runcinated 5-orthoplex Small prismated triacontiditeron (spat) |
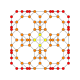
| 17 |  |
 |
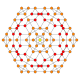 |
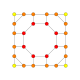 |
|
t0,1,2{4,3,3,3} = tr{4,3,3,3} Cantitruncated 5-cube Great rhombated penteract (girn) |
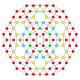
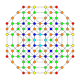
| 18 |  |
 |
 |
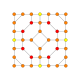 |
|
t1,2,3{4,3,3,3} = tr{4,3,3,3} Bicantitruncated 5-cube Great birhombi-penteractitriacontiditeron (gibrant) |
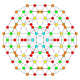
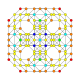
| 19 |  |
 |
 |
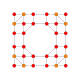 |
|
t0,1,3{4,3,3,3} Runcitruncated 5-cube Prismatotruncated penteract (pattin) |
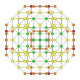
| 20 |  |
 |
 |
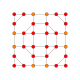 |
|
t0,2,3{4,3,3,3} Runcicantellated 5-cube Prismatorhomated penteract (prin) |
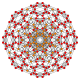
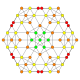
| 21 |  |
 |
 |
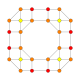 |
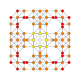
|
t0,1,4{4,3,3,3} Steritruncated 5-cube Cellitruncated penteract (capt) |
| 22 |  |
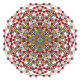 |
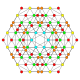 |
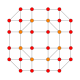 |
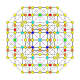
|
t0,2,4{4,3,3,3} Stericantellated 5-cube Cellirhombi-penteractitriacontiditeron (carnit) |
| 23 |  |
 |
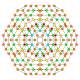 |
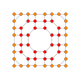 |
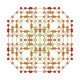
|
t0,1,2,3{4,3,3,3} Runcicantitruncated 5-cube Great primated penteract (gippin) |
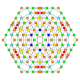
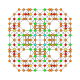
| 24 |  |
 |
 |
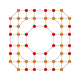 |
|
t0,1,2,4{4,3,3,3} Stericantitruncated 5-cube Celligreatorhombated penteract (cogrin) |
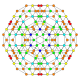
| 25 |  |
 |
 |
 |
|
t0,1,3,4{4,3,3,3} Steriruncitruncated 5-cube Celliprismatotrunki-penteractitriacontiditeron (captint) |
| 26 |  |
 |
 |
 |
|
t0,1,2,3,4{4,3,3,3} Omnitruncated 5-cube Great celli-penteractitriacontiditeron (gacnet) |
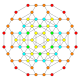
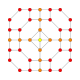
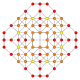
| 27 |  |
 |
 |
 |
|
t0,1,2{3,3,3,4} = tr{3,3,3,4} Cantitruncated 5-orthoplex Great rhombated triacontiditeron (gart) |
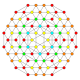
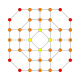
| 28 |  |
 |
 |
 |
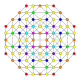
|
t0,1,3{3,3,3,4} Runcitruncated 5-orthoplex Prismatotruncated triacontiditeron (pattit) |
| 29 |  |
 |
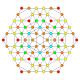 |
 |

|
t0,2,3{3,3,3,4} Runcicantellated 5-orthoplex Prismatorhombated triacontiditeron (pirt) |
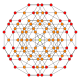
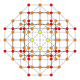
| 30 |  |
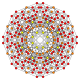 |
 |
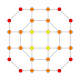 |
|
t0,1,4{3,3,3,4} Steritruncated 5-orthoplex Cellitruncated triacontiditeron (cappin) |
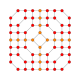
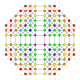
| 31 |  |
 |
 |
 |
|
t0,1,2,3{3,3,3,4} Runcicantitruncated 5-orthoplex Great prismatorhombated triacontiditeron (gippit) |
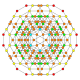
| 32 |  |
 |
 |
 |

|
t0,1,2,4{3,3,3,4} Stericantitruncated 5-orthoplex Celligreatorhombated triacontiditeron (cogart) |
References
[edit]- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6[1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
External links
[edit]- Klitzing, Richard. "5D uniform polytopes (polytera)".
