Adatom

Adatom according to the TLK model

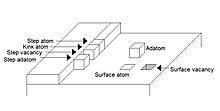
An adatom is an atom that lies on a crystal surface, and can be thought of as the opposite of a surface vacancy. This term is used in surface chemistry and epitaxy, when describing single atoms lying on surfaces and surface roughness. The word is a portmanteau of "adsorbed atom". A single atom, a cluster of atoms, or a molecule or cluster of molecules may all be referred to by the general term "adparticle". This is often a thermodynamically unfavorable state. However, cases such as graphene may provide counter-examples.

Growth

″Adatom″ is a portmanteau word, short for adsorbed atom. When the atom arrives at a crystal surface, it is adsorbed by the periodic potential of the crystal, thus becoming an adatom. The minima of this potential form a network of adsorption sites on the surface. There are different types of adsorption sites. Each of these sites corresponds to a different structure of the surface. There are five different types of adsorption sites, which are: on a terrace, where the adsorption site is on top of the surface layer that is growing; at the step edge, which is next to the growing layer; in the kink of a growing layer; in the step edge of a growing layer, and in the surface layer, where the adsorption site is inside the lower layer.

Out of these adsorption site types, kink sites play the most important role in crystal growth. Kink density is a major factor of growth kinetics. Attachment of an atom to the kink site, or removal of the atom from the kink, does not change the free surface energy of the crystal, since the number of broken bonds does not change. This gives that the chemical potential of an atom in the kink site is equal to that of the crystal, which means that the kink site is the one adsorption site type where an adatom becomes a part of the crystal.

If crystallography is used, or if the growth temperatures are higher, which would give an entropy effect, the crystal surface becomes rough, causing greater number of kinks. This means that adatoms have a greater chance of arriving at a kink site, to become part of the crystal. This is the normal mechanism of growth.

The opposite, so with a lower growth temperature, would give a smooth surface, which means that there is a higher number of terrace adsorption sites. There are still kink sites, but these are only found at the edges of steps. The crystal only grows through "lateral motion of the steps". This type of growth is called the layer mechanism of growth. How the adatoms grow on the surface depends on what interaction is the strongest or what the surface looks like. If the adatom-adatom interaction is the strongest, adatoms are more likely to create pyramids of adatoms on the surface. If the adatom-surface interaction is the strongest, the adatoms are more likely to arrange themselves in such a way as to create layers on the surface. But it also depends on the origins of the steps on the surface. In total there are five different types of layer growth: normal growth, step-flow growth, layer-by-layer growth, multilayer (or three-dimensional island) growth, and spiral growth.

Step-flow growth is observed on stair-like surfaces. These surfaces have a geometry with vicinal steps separated by "atomically flat low-index terraces". When adatoms attach to the edges of the steps, they move along the surface, until they find a kink site to attach to become part of the crystal. However, if the kink density is not high enough, and thus not all adatoms arrive at one of the kinks, additional steps, as if there is a flat surface with small two-dimensional islands on it, are created on the terraces, leading to a mixed growth mode, which leads to a change in layer growth type, from step-flow to layer-by-layer growth.

In layer-by-layer growth, the adatom-surface interaction is the strongest. A new layer is created through 2D islands, which is created on the surface. The islands grow until they spread out over the entire surface, and the next layer will start to grow. This growth is named Frank-Van der Merwe (FM) growth.

In some cases the cycle of making new layers in layer-by-layer growth is broken by kinetic constraints. In these cases, growth in higher layers starts before lower layers are finished, which means three-dimensional island are created. A new type of growth, called multilayer growth, is started, instead of the layer-by-layer growth. Multilayer growth can be divided into Volmer-Weber growth and Stranski-Krastanov growth.

If the crystal surface contains a screw dislocation, a different type of growth, called spiral growth might take place. Around the screw dislocation, a spiral shape is seen during growth. As the screw dislocation causes a growth spiral that does not disappear, islands might not be needed to cause crystal growth.

The adatoms are bound to the surface through epitaxy. In this process, new layers of a crystal are created through the attachment of new atoms. This can be through a chemical reaction, or through heating a new film or centrifuging it. Generally, what happens is that the particles that are used to form a new layer, will not always be adsorbed. To create bonds with the surface, energy is needed and not every particle has the needed amount of energy to attach at that part of the surface (for different parts, different energies are needed). If one has a flux F of particles incoming, part of it will be adsorbed, given by the adsorption flux

$J_{ads}=sF$

where s here is the sticking coefficient. Not only does this variable depend on the surface and on the energy of the incoming atom, but also on the chemical nature of both the particle and the surface. If both the particle and surface are made of a substance that easily reacts with other particles, it is easier for the atoms to stick to the surface.

Surface thermodynamics

Taking a look at the thermodynamics at the surface of the film, it is seen that bonds are broken, releasing energy, and bonds are formed, confining energy. The thermodynamics involved were modeled by the Walther Kossel and Ivan Stranski in 1920. This model is called terrace ledge kink model (TLK).

The adatom can create more than one bond with the crystal, depending on the structure of the crystal. If it is a simple cubic lattice, the adatom can have up to 6 bonds, whereas in a face-centered cubic lattice, it can have up to 12 nearest neighbors. The more bonds created, the more energy is confined, making it harder to desorb the adatom.

A special site for an adatom is a kink, where exactly half of the bonds with the surface can be created, also called the "half-crystal position".

Magnetic adatoms

Adatoms, due to having fewer bonds than the other atoms in the crystal, have unbound electrons. These electrons have spin and therefore a magnetic moment. This magnetic moment has no preference for orientation until an external influence, like a magnetic field, is present. The structure of the adatoms on a surface can be adjusted by changing the external magnetic field. Through this method theoretical situations, such as the atomic chain, can be simulated. Quantum mechanics needs to be taken into account when using adatoms due to the small scale.

The magnetic field created by an atom is caused mostly by the orbit and spin of the electrons. The proton's and neutron's magnetic moment are negligible when compared to that of the electron due to their larger masses. When an atom with free electrons is inside an external magnetic field, its magnetic moment aligns with the external field because this lowers its energy. This is why bound electrons do not display this magnetic moment, they already have a favorable energy state and it is unfavorable to change. The magnetization of an (magnetically aligned) atom is given by:

$M={\frac {Ng_{j}^{2}\mu _{B}^{2}B}{3k_{b}T}}j(j+1)$

Where N is the number of electrons, g_j is the g-factor, μ_B is the Bohr magneton, k_b is the Boltzmann constant, T is the temperature and j is the total angular momentum quantum number. This formula holds under the assumption that the magnetic energy of an electron is given by $E=m_{j}g_{j}\mu _{B}B$ and there is no exchange interaction.

Movement across a surface

The movement of adatoms across a surface can be described by the Burton, Cabrera and Frank (CBF) model. The model treats adatoms as a 2D gas on top of the surface. The adatoms diffuse with a diffusion constant D; they are desorbed back to the medium above with a rate of $1/\tau _{des}$ per atom and adsorbed with flux F.

The diffusion constant can be, when the concentration of particles is small, expressed as:

$D={\frac {1}{4}}a^{2}\nu _{0}{\text{exp}}(-{\frac {E_{D}}{k_{b}T}})$

Where a is the hopping distance for the atom. E_D is the energy needed to pass the diffusion barrier. ν₀ is the attempt frequency.

The CBF model obeys the following continuity equation:

${\frac {\partial n}{\partial t}}=D\nabla ^{2}n+F-{\frac {n}{\tau _{des}}}$

Combining the steady states ($dn/dt=0$) with the following boundary conditions can lead to an expression for the velocity of the adatoms at each adsorption site.

$\nu _{i}=\beta _{inc}[n_{1}(x_{i})-{\tilde {n}}]+\beta _{inc}[n_{u}(x_{i})-{\tilde {n}}]$

The boundary conditions:

$D{\frac {\mathrm {d} n_{1}}{\mathrm {d} x}}|_{x=x_{i}}=\beta _{inc}[n_{1}(x_{i})-{\tilde {n}}]+\beta _{p}[n_{1}(x_{1})-n_{u}(x_{i})]$

And:

$-D{\frac {\mathrm {d} n_{u}}{\mathrm {d} x}}|_{x=x_{i}}=\beta _{inc}[n_{u}(x_{i})-{\tilde {n}}]+\beta _{p}[n_{1}(x_{1})-n_{u}(x_{i})]$

Applications

In 2012, scientists at the University of New South Wales were able to use phosphine to precisely, deterministically eject a single silicon atom onto a surface of epitaxial silicon. This resulting adatom created what is described as a single-atom transistor. Thus, inasmuch as chemical empirical formulas pinpoint the locations of branching ions that are attached to a particular molecule, the dopant of silicon based transistors and other such electronic components will have the location identified of each dopant atom or molecule, along with the associated characteristic of the device based on the named locations. Thus, the mapping of the dopant substances will give exact characteristics of any given semiconductor device, once all is known.

With the technology available nowadays it is possible to create a linear chain of adatoms on top of an epitaxial film. With this, one can analyse theoretical situations.

Furthermore, Usami et al. were able to create quantum wells by adding Si atoms to a SiGe bulk crystal. Within these wells they observed photoluminescence of excitons that were confined in these wells.