ABACABA pattern
Appearance

The ABACABA pattern is a recursive fractal pattern that shows up in many places in the real world (such as in geometry, art, music, poetry, number systems, literature and higher dimensions).[1][2][3][4] Patterns often show a DABACABA type subset. AA, ABBA, and ABAABA type forms are also considered.[5]
Generating the pattern
[edit]In order to generate the next sequence, first take the previous pattern, add the next letter from the alphabet, and then repeat the previous pattern. The first few steps are listed here.[4]
| Step | Pattern | Letters |
|---|---|---|
| 1 | A | 21 − 1 = 1 |
| 2 | ABA | 3 |
| 3 | ABACABA | 7 |
| 4 | ABACABADABACABA | 15 |
| 5 | ABACABADABACABAEABACABADABACABA | 31 |
| 6 | ABACABADABACABAEABACABADABACABAFABACABADABACABAEABACABADABACABA | 63 |
ABACABA is a "quickly growing word", often described as chiastic or "symmetrically organized around a central axis" (see: Chiastic structure and Χ).[4] The number of members in each iteration is a(n) = 2n − 1, the Mersenne numbers (OEIS: A000225).
Gallery
[edit]-
Metric levels:[1]EABACABADABACABA
-
A staircase built with the largest possible squares/cubes while allowing equally sized steps:ABACABADABACABA[1]
-
Binary-reflected Gray code (BRGC):to G
-
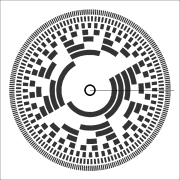
Rotary encoder:to I
-
3-bit Gray code visualized as a traversal of vertices of a cube (0,1,3,2,6,7,5,4):[1]ABACABA
-
Château de Chambord:ABACABA[6]
See also
[edit]Notes
[edit]- ^ The strength, emphasis, or importance of the beginning of each duration the length of a single measure in 4
4 (eighth-notes) is, divisively (, , ), determined by each eighth-note's position in a DABACABA structure, while the eighth notes of two measures grouped, additively (), are determined by an EABACABADABACABA structure.[3]
References
[edit]- ^ a b c d e f g h i j k l m Naylor, Mike (February 2013). "ABACABA Amazing Pattern, Amazing Connections". Math Horizons. Retrieved June 13, 2019.
- ^ a b c d SheriOZ (2016-04-21). "Exploring Fractals with ABACABA". Chicago Geek Guy. Archived from the original on 22 January 2021. Retrieved January 22, 2021.
- ^ a b Naylor, Mike (2011). "Abacaba! – Using a mathematical pattern to connect art, music, poetry and literature" (PDF). Bridges. Retrieved October 6, 2017.
- ^ a b c Conley, Craig (2008-10-01). Magic Words: A Dictionary. Weiser Books. p. 53. ISBN 9781609250508.
- ^ Halter-Koch, Franz and Tichy, Robert F.; eds. (2000). Algebraic Number Theory and Diophantine Analysis, p.478. W. de Gruyter. ISBN 9783110163049.
- ^ Wright, Craig (2016). Listening to Western Music, p.48. Cengage Learning. ISBN 9781305887039.
External links
[edit]- Naylor, Mike: abacaba.org

![Sierpinski triangle[1][2]: ABACABA](http://upload.wikimedia.org/wikipedia/commons/thumb/b/bb/ABACABA_Sierpinski_triangle.svg/180px-ABACABA_Sierpinski_triangle.svg.png)
![Ruler,[1][2] excluding 1 and 2: ABACABADABACABA excluding 2: EABACABADABACABA](http://upload.wikimedia.org/wikipedia/commons/thumb/7/7d/Measuring_-_Fractions_of_an_inch.svg/180px-Measuring_-_Fractions_of_an_inch.svg.png)
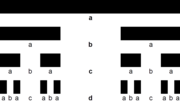
![Binary tree[1][2]/upside down family tree: ABACABADABACABA](http://upload.wikimedia.org/wikipedia/commons/thumb/e/e6/Ex_001.png/180px-Ex_001.png)
![Koch curve:[1] '"`UNIQ--postMath-00000001-QINU`"' is ABA, '"`UNIQ--postMath-00000002-QINU`"' is ABACABA, and '"`UNIQ--postMath-00000003-QINU`"': ABACABADABACABA](http://upload.wikimedia.org/wikipedia/commons/thumb/1/1a/KochCurve1_abacaba_pattern.png/125px-KochCurve1_abacaba_pattern.png)



![Metric hierarchy: ABACABADABACABA[a]](http://upload.wikimedia.org/wikipedia/commons/thumb/a/ad/Solfege_subdivision_de_la_ronde_a_la_croche.svg/180px-Solfege_subdivision_de_la_ronde_a_la_croche.svg.png)
![Metric levels:[1] EABACABADABACABA](http://upload.wikimedia.org/wikipedia/commons/thumb/8/82/Metric_levels.svg/180px-Metric_levels.svg.png)
![A staircase built with the largest possible squares/cubes while allowing equally sized steps: ABACABADABACABA[1]](http://upload.wikimedia.org/wikipedia/commons/thumb/d/db/Staircase_of_largest_squares_abacaba_pattern.svg/180px-Staircase_of_largest_squares_abacaba_pattern.svg.png)
![A "circle fractal"[1] superimposed with a 2 × 2 box fractal: ABACABADABACABA](http://upload.wikimedia.org/wikipedia/commons/thumb/7/72/Circle-box_fractal_abacaba_pattern.svg/180px-Circle-box_fractal_abacaba_pattern.svg.png)
![The Tower of Hanoi[1] with four disks: ABACABADABACABA](http://upload.wikimedia.org/wikipedia/commons/thumb/2/20/Tower_of_Hanoi_recursion_SMIL.svg/120px-Tower_of_Hanoi_recursion_SMIL.svg.png)


![3-bit Gray code visualized as a traversal of vertices of a cube (0,1,3,2,6,7,5,4):[1] ABACABA](http://upload.wikimedia.org/wikipedia/commons/thumb/4/4f/Blue_cube_with_Gray_code_path.png/171px-Blue_cube_with_Gray_code_path.png)
![Château de Chambord: ABACABA[6]](http://upload.wikimedia.org/wikipedia/commons/thumb/4/47/Chambord_Castle_Northwest_facade.jpg/180px-Chambord_Castle_Northwest_facade.jpg)
![Gray code along the number line[1] (OEIS: A003188): ABACABADABACABAEABACABADABACABA](http://upload.wikimedia.org/wikipedia/commons/thumb/b/bd/Gray_code_number_line_arcs.svg/180px-Gray_code_number_line_arcs.svg.png)
![Devil's needle:[1] ABACABADABACABA](http://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Baguenaudier.svg/180px-Baguenaudier.svg.png)





