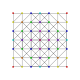A8 polytope

Orthographic projections
A₈ Coxeter plane

8-simplex

In 8-dimensional geometry, there are 135 uniform polytopes with A₈ symmetry. There is one self-dual regular form, the 8-simplex with 9 vertices.

Each can be visualized as symmetric orthographic projections in Coxeter planes of the A₈ Coxeter group, and other subgroups.

Graphs

Symmetric orthographic projections of these 135 polytopes can be made in the A₈, A₇, A₆, A₅, A₄, A₃, A₂ Coxeter planes. A_k has [k+1] symmetry.

These 135 polytopes are each shown in these 7 symmetry planes, with vertices and edges drawn, and vertices colored by the number of overlapping vertices in each projective position.

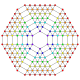
#	Coxeter-Dynkin diagram Schläfli symbol Johnson name	Ak orthogonal projection graphs
		A8 [9]	A7 [8]	A6 [7]	A5 [6]	A4 [5]	A3 [4]	A2 [3]
1	t0{3,3,3,3,3,3,3} 8-simplex
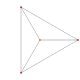
2	t1{3,3,3,3,3,3,3} Rectified 8-simplex
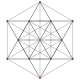
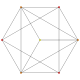
3	t2{3,3,3,3,3,3,3} Birectified 8-simplex
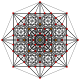
4	t3{3,3,3,3,3,3,3} Trirectified 8-simplex
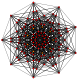
5	t0,1{3,3,3,3,3,3,3} Truncated 8-simplex
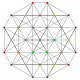
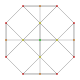
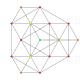
6	t0,2{3,3,3,3,3,3,3} Cantellated 8-simplex
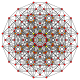
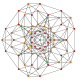
7	t1,2{3,3,3,3,3,3,3} Bitruncated 8-simplex
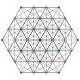
8	t0,3{3,3,3,3,3,3,3} Runcinated 8-simplex
9	t1,3{3,3,3,3,3,3,3} Bicantellated 8-simplex
10	t2,3{3,3,3,3,3,3,3} Tritruncated 8-simplex
11	t0,4{3,3,3,3,3,3,3} Stericated 8-simplex
12	t1,4{3,3,3,3,3,3,3} Biruncinated 8-simplex
13	t2,4{3,3,3,3,3,3,3} Tricantellated 8-simplex
14	t3,4{3,3,3,3,3,3,3} Quadritruncated 8-simplex
15	t0,5{3,3,3,3,3,3,3} Pentellated 8-simplex
16	t1,5{3,3,3,3,3,3,3} Bistericated 8-simplex
17	t2,5{3,3,3,3,3,3,3} Triruncinated 8-simplex
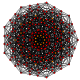
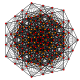
18	t0,6{3,3,3,3,3,3,3} Hexicated 8-simplex
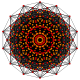
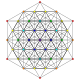
19	t1,6{3,3,3,3,3,3,3} Bipentellated 8-simplex
20	t0,7{3,3,3,3,3,3,3} Heptellated 8-simplex
21	t0,1,2{3,3,3,3,3,3,3} Cantitruncated 8-simplex
22	t0,1,3{3,3,3,3,3,3,3} Runcitruncated 8-simplex
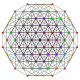
23	t0,2,3{3,3,3,3,3,3,3} Runcicantellated 8-simplex
24	t1,2,3{3,3,3,3,3,3,3} Bicantitruncated 8-simplex
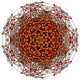
25	t0,1,4{3,3,3,3,3,3,3} Steritruncated 8-simplex
26	t0,2,4{3,3,3,3,3,3,3} Stericantellated 8-simplex
27	t1,2,4{3,3,3,3,3,3,3} Biruncitruncated 8-simplex
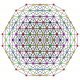
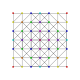
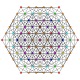
28	t0,3,4{3,3,3,3,3,3,3} Steriruncinated 8-simplex
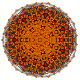
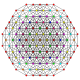
29	t1,3,4{3,3,3,3,3,3,3} Biruncicantellated 8-simplex
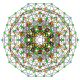
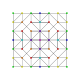
30	t2,3,4{3,3,3,3,3,3,3} Tricantitruncated 8-simplex
31	t0,1,5{3,3,3,3,3,3,3} Pentitruncated 8-simplex
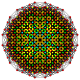
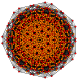
32	t0,2,5{3,3,3,3,3,3,3} Penticantellated 8-simplex
33	t1,2,5{3,3,3,3,3,3,3} Bisteritruncated 8-simplex
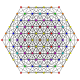
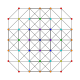
34	t0,3,5{3,3,3,3,3,3,3} Pentiruncinated 8-simplex
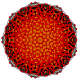
35	t1,3,5{3,3,3,3,3,3,3} Bistericantellated 8-simplex
36	t2,3,5{3,3,3,3,3,3,3} Triruncitruncated 8-simplex
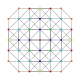
37	t0,4,5{3,3,3,3,3,3,3} Pentistericated 8-simplex
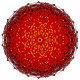
38	t1,4,5{3,3,3,3,3,3,3} Bisteriruncinated 8-simplex
39	t0,1,6{3,3,3,3,3,3,3} Hexitruncated 8-simplex
40	t0,2,6{3,3,3,3,3,3,3} Hexicantellated 8-simplex
41	t1,2,6{3,3,3,3,3,3,3} Bipentitruncated 8-simplex
42	t0,3,6{3,3,3,3,3,3,3} Hexiruncinated 8-simplex
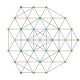
43	t1,3,6{3,3,3,3,3,3,3} Bipenticantellated 8-simplex
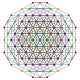
44	t0,4,6{3,3,3,3,3,3,3} Hexistericated 8-simplex
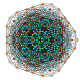
45	t0,5,6{3,3,3,3,3,3,3} Hexipentellated 8-simplex
46	t0,1,7{3,3,3,3,3,3,3} Heptitruncated 8-simplex
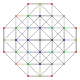
47	t0,2,7{3,3,3,3,3,3,3} Hepticantellated 8-simplex
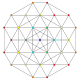
48	t0,3,7{3,3,3,3,3,3,3} Heptiruncinated 8-simplex
49	t0,1,2,3{3,3,3,3,3,3,3} Runcicantitruncated 8-simplex
50	t0,1,2,4{3,3,3,3,3,3,3} Stericantitruncated 8-simplex
51	t0,1,3,4{3,3,3,3,3,3,3} Steriruncitruncated 8-simplex
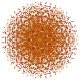
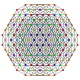
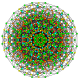
52	t0,2,3,4{3,3,3,3,3,3,3} Steriruncicantellated 8-simplex
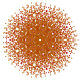
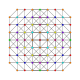
53	t1,2,3,4{3,3,3,3,3,3,3} Biruncicantitruncated 8-simplex
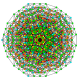
54	t0,1,2,5{3,3,3,3,3,3,3} Penticantitruncated 8-simplex
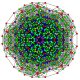
55	t0,1,3,5{3,3,3,3,3,3,3} Pentiruncitruncated 8-simplex
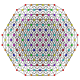
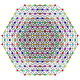
56	t0,2,3,5{3,3,3,3,3,3,3} Pentiruncicantellated 8-simplex
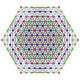
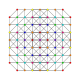
57	t1,2,3,5{3,3,3,3,3,3,3} Bistericantitruncated 8-simplex
58	t0,1,4,5{3,3,3,3,3,3,3} Pentisteritruncated 8-simplex
59	t0,2,4,5{3,3,3,3,3,3,3} Pentistericantellated 8-simplex
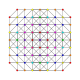
60	t1,2,4,5{3,3,3,3,3,3,3} Bisteriruncitruncated 8-simplex
61	t0,3,4,5{3,3,3,3,3,3,3} Pentisteriruncinated 8-simplex
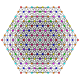
62	t1,3,4,5{3,3,3,3,3,3,3} Bisteriruncicantellated 8-simplex
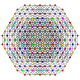
63	t2,3,4,5{3,3,3,3,3,3,3} Triruncicantitruncated 8-simplex
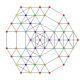
64	t0,1,2,6{3,3,3,3,3,3,3} Hexicantitruncated 8-simplex
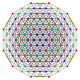
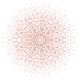
65	t0,1,3,6{3,3,3,3,3,3,3} Hexiruncitruncated 8-simplex
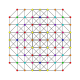
66	t0,2,3,6{3,3,3,3,3,3,3} Hexiruncicantellated 8-simplex
67	t1,2,3,6{3,3,3,3,3,3,3} Bipenticantitruncated 8-simplex
68	t0,1,4,6{3,3,3,3,3,3,3} Hexisteritruncated 8-simplex
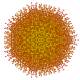
69	t0,2,4,6{3,3,3,3,3,3,3} Hexistericantellated 8-simplex
70	t1,2,4,6{3,3,3,3,3,3,3} Bipentiruncitruncated 8-simplex
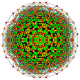
71	t0,3,4,6{3,3,3,3,3,3,3} Hexisteriruncinated 8-simplex
72	t1,3,4,6{3,3,3,3,3,3,3} Bipentiruncicantellated 8-simplex
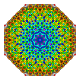
73	t0,1,5,6{3,3,3,3,3,3,3} Hexipentitruncated 8-simplex
74	t0,2,5,6{3,3,3,3,3,3,3} Hexipenticantellated 8-simplex
75	t1,2,5,6{3,3,3,3,3,3,3} Bipentisteritruncated 8-simplex
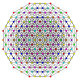
76	t0,3,5,6{3,3,3,3,3,3,3} Hexipentiruncinated 8-simplex
77	t0,4,5,6{3,3,3,3,3,3,3} Hexipentistericated 8-simplex
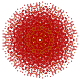
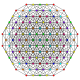
78	t0,1,2,7{3,3,3,3,3,3,3} Hepticantitruncated 8-simplex
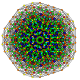
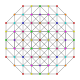
79	t0,1,3,7{3,3,3,3,3,3,3} Heptiruncitruncated 8-simplex
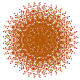
80	t0,2,3,7{3,3,3,3,3,3,3} Heptiruncicantellated 8-simplex
81	t0,1,4,7{3,3,3,3,3,3,3} Heptisteritruncated 8-simplex
82	t0,2,4,7{3,3,3,3,3,3,3} Heptistericantellated 8-simplex
83	t0,3,4,7{3,3,3,3,3,3,3} Heptisteriruncinated 8-simplex
84	t0,1,5,7{3,3,3,3,3,3,3} Heptipentitruncated 8-simplex
85	t0,2,5,7{3,3,3,3,3,3,3} Heptipenticantellated 8-simplex
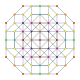
86	t0,1,6,7{3,3,3,3,3,3,3} Heptihexitruncated 8-simplex
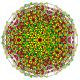
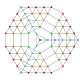
87	t0,1,2,3,4{3,3,3,3,3,3,3} Steriruncicantitruncated 8-simplex
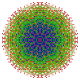
88	t0,1,2,3,5{3,3,3,3,3,3,3} Pentiruncicantitruncated 8-simplex
89	t0,1,2,4,5{3,3,3,3,3,3,3} Pentistericantitruncated 8-simplex
90	t0,1,3,4,5{3,3,3,3,3,3,3} Pentisteriruncitruncated 8-simplex
91	t0,2,3,4,5{3,3,3,3,3,3,3} Pentisteriruncicantellated 8-simplex
92	t1,2,3,4,5{3,3,3,3,3,3,3} Bisteriruncicantitruncated 8-simplex
93	t0,1,2,3,6{3,3,3,3,3,3,3} Hexiruncicantitruncated 8-simplex
94	t0,1,2,4,6{3,3,3,3,3,3,3} Hexistericantitruncated 8-simplex
95	t0,1,3,4,6{3,3,3,3,3,3,3} Hexisteriruncitruncated 8-simplex
96	t0,2,3,4,6{3,3,3,3,3,3,3} Hexisteriruncicantellated 8-simplex
97	t1,2,3,4,6{3,3,3,3,3,3,3} Bipentiruncicantitruncated 8-simplex
98	t0,1,2,5,6{3,3,3,3,3,3,3} Hexipenticantitruncated 8-simplex
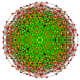
99	t0,1,3,5,6{3,3,3,3,3,3,3} Hexipentiruncitruncated 8-simplex
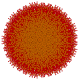
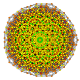
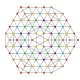
100	t0,2,3,5,6{3,3,3,3,3,3,3} Hexipentiruncicantellated 8-simplex
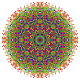
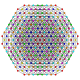
101	t1,2,3,5,6{3,3,3,3,3,3,3} Bipentistericantitruncated 8-simplex
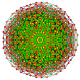
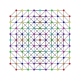
102	t0,1,4,5,6{3,3,3,3,3,3,3} Hexipentisteritruncated 8-simplex
103	t0,2,4,5,6{3,3,3,3,3,3,3} Hexipentistericantellated 8-simplex
104	t0,3,4,5,6{3,3,3,3,3,3,3} Hexipentisteriruncinated 8-simplex
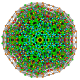
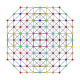
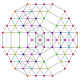
105	t0,1,2,3,7{3,3,3,3,3,3,3} Heptiruncicantitruncated 8-simplex
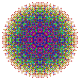
106	t0,1,2,4,7{3,3,3,3,3,3,3} Heptistericantitruncated 8-simplex
107	t0,1,3,4,7{3,3,3,3,3,3,3} Heptisteriruncitruncated 8-simplex
108	t0,2,3,4,7{3,3,3,3,3,3,3} Heptisteriruncicantellated 8-simplex
109	t0,1,2,5,7{3,3,3,3,3,3,3} Heptipenticantitruncated 8-simplex
110	t0,1,3,5,7{3,3,3,3,3,3,3} Heptipentiruncitruncated 8-simplex
111	t0,2,3,5,7{3,3,3,3,3,3,3} Heptipentiruncicantellated 8-simplex
112	t0,1,4,5,7{3,3,3,3,3,3,3} Heptipentisteritruncated 8-simplex
113	t0,1,2,6,7{3,3,3,3,3,3,3} Heptihexicantitruncated 8-simplex
114	t0,1,3,6,7{3,3,3,3,3,3,3} Heptihexiruncitruncated 8-simplex
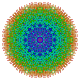
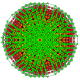
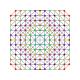
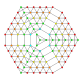
115	t0,1,2,3,4,5{3,3,3,3,3,3,3} Pentisteriruncicantitruncated 8-simplex
116	t0,1,2,3,4,6{3,3,3,3,3,3,3} Hexisteriruncicantitruncated 8-simplex
117	t0,1,2,3,5,6{3,3,3,3,3,3,3} Hexipentiruncicantitruncated 8-simplex
118	t0,1,2,4,5,6{3,3,3,3,3,3,3} Hexipentistericantitruncated 8-simplex
119	t0,1,3,4,5,6{3,3,3,3,3,3,3} Hexipentisteriruncitruncated 8-simplex
120	t0,2,3,4,5,6{3,3,3,3,3,3,3} Hexipentisteriruncicantellated 8-simplex
121	t1,2,3,4,5,6{3,3,3,3,3,3,3} Bipentisteriruncicantitruncated 8-simplex
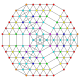
122	t0,1,2,3,4,7{3,3,3,3,3,3,3} Heptisteriruncicantitruncated 8-simplex
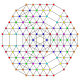
123	t0,1,2,3,5,7{3,3,3,3,3,3,3} Heptipentiruncicantitruncated 8-simplex
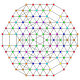
124	t0,1,2,4,5,7{3,3,3,3,3,3,3} Heptipentistericantitruncated 8-simplex
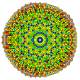
125	t0,1,3,4,5,7{3,3,3,3,3,3,3} Heptipentisteriruncitruncated 8-simplex
126	t0,2,3,4,5,7{3,3,3,3,3,3,3} Heptipentisteriruncicantellated 8-simplex
127	t0,1,2,3,6,7{3,3,3,3,3,3,3} Heptihexiruncicantitruncated 8-simplex
128	t0,1,2,4,6,7{3,3,3,3,3,3,3} Heptihexistericantitruncated 8-simplex
129	t0,1,3,4,6,7{3,3,3,3,3,3,3} Heptihexisteriruncitruncated 8-simplex
130	t0,1,2,5,6,7{3,3,3,3,3,3,3} Heptihexipenticantitruncated 8-simplex
131	t0,1,2,3,4,5,6{3,3,3,3,3,3,3} Hexipentisteriruncicantitruncated 8-simplex
132	t0,1,2,3,4,5,7{3,3,3,3,3,3,3} Heptipentisteriruncicantitruncated 8-simplex
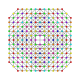
133	t0,1,2,3,4,6,7{3,3,3,3,3,3,3} Heptihexisteriruncicantitruncated 8-simplex
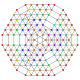
134	t0,1,2,3,5,6,7{3,3,3,3,3,3,3} Heptihexipentiruncicantitruncated 8-simplex
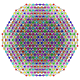
135	t0,1,2,3,4,5,6,7{3,3,3,3,3,3,3} Omnitruncated 8-simplex

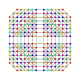
References

• H.S.M. Coxeter:
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
  • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966

External links

• Klitzing, Richard. "8D uniform polytopes (polyzetta)".