User:Retired Pchem Prof/JouleThomson

This is my personal work space for work in progress. You are welcome to read here and comment on the associated talk page. If you must, you may insert comments or suggested text, but please make such insertions obvious (bold text, for example) and call them to my attention on the talk page. And please do not delete anything here (I know it is retrievable, but I haven't figured out how to do that yet).

Underway here are revisions to the article on the Joule–Thomson effect.

Description

The adiabatic (no heat exchanged) expansion of a gas may be carried out in a number of ways. The change in temperature experienced by the gas during expansion depends not only on the initial and final pressure, but also on the manner in which the expansion is carried out.

If the expansion process is reversible, meaning that the gas is in thermodynamic equilibrium at all times, it is called an isentropic expansion. In this scenario, the gas does positive work during the expansion, and its temperature decreases.

In a free expansion, on the other hand, the gas does no work and absorbs no heat, so the internal energy is conserved. Expanded in this manner, the temperature of an ideal gas would remain constant, but the temperature of a real gas decreases, except at very high temperature. ^[1]

The method of expansion discussed in this article, in which a gas or liquid at pressure P₁ flows into a region of lower pressure P₂ without significant change in kinetic energy, is called the Joule–Thomson expansion. The expansion is inherently irreversible; that is, there can be no such thing as a Joule-Thompson compression. During this expansion, enthalpy remains unchanged (see proof below). Unlike a free expansion, work is done, causing a change in internal energy. Whether the internal energy increases or decreases is determined by whether work is done on or by the fluid; that is determined by the initial and final states of the expansion and the properties of the fluid.

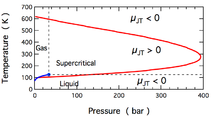
The temperature change produced during a Joule-Thomson expansion is quantified by the Joule–Thomson coefficient, $\mu _{\mathrm {JT} }$ . This coefficient may be either positive (corresponding to cooling) or negative (heating); the regions where each occurs for molecular nitrogen, N₂, are shown in the figure. Note that most conditions in the figure correspond to N₂ being a supercritical fluid, where it has some properties of a gas and some of a liquid, but can not be really described as being either. The coefficient is negative at both very high and very low temperatures; at very high pressure it is negative at all temperatures. The maximum inversion temperature (621 K for N₂^[2]) occurs as zero pressure is approached. For N₂ gas at low pressures, $\mu _{\mathrm {JT} }$ is negative at high temperatures and positive at low temperatures. At temperatures below the gas-liquid coexistence curve, N₂ condenses to form a liquid and the coefficient again becomes negative. Thus, for N₂ gas below 621 K, a Joule-Thomson expansion can be used to cool the gas until liquid N₂ forms.

Physical mechanism (new version)

There are two factors that can change the temperature of a fluid during an adiabatic expansion: a change in internal energy or the conversion between potential and kinetic internal energy. Temperature is the measure of thermal kinetic energy (energy associated with molecular motion); so a change in temperature indicates a change in thermal kinetic energy. The internal energy is the sum of thermal kinetic energy and thermal potential energy.^[3] Thus, even if the internal energy does not change, the temperature can change due to conversion between kinetic and potential energy; this is what happens in a free expansion and typically produces a decrease in temperature as the fluid expands.^[4]^[5] If work is done on or by the fluid as it expands, then the total internal energy changes. This is what happens in a Joule-Thomson expansion and can produce larger heating or cooling than observed in a free expansion.

In a Joule-Thomson expansion the enthalpy remains constant. The enthalpy, $H$ , is defined as

H=U+PV

where $U$ is internal energy, $P$ is pressure, and $V$ is volume. Under the conditions of a Joule-Thomson expansion, the change in $PV$ represents the work done by the fluid (see the proof below). If $PV$ increases, with $H$ constant, then $U$ must decrease as a result of the fluid doing work on its surroundings. This produces a decrease in temperature and results in a positive Joule-Thomson coefficient. Conversely, a decrease in $PV$ means that work is done on the fluid and the internal energy increases. If the increase in internal energy exceeds the increase in potential energy, there will be an increase in the temperature of the fluid and the Joule-Thomson coefficient will be negative.

For an ideal gas, $PV$ does not change during a Joule-Thomson expansion.^[6] As a result, there is no change in internal energy; since there is also no change in thermal potential energy, there can be no change in thermal kinetic energy and, therefore, no change in temperature. In real gases, $PV$ does change.

The ratio of the value of $PV$ to that expected for an ideal gas at the same temperature is called the compressibility factor, $Z$ . For a gas, this is typically less than unity at low temperature and greater than unity at high temperature (see the discussion in compressibility factor). At low pressure, the value of $Z$ always moves towards unity as a gas expands.^[7] Thus at low temperature, $Z$ and $PV$ will increase as the gas expands, resulting in a positive Joule-Thomson coefficient. At high temperature, $Z$ and $PV$ decrease as the gas expands; if the decrease is large enough, the Joule-Thomson coefficient will be negative.

For liquids, and for supercritical fluids under high pressure, $PV$ increases as pressure increases.^[7] This is due to molecules being forced together, so that the volume can barely decrease due to higher pressure. Under such conditions, the Joule-Thomson coefficient is negative, as seen in the figure above.

Applications

The cooling produced in the Joule–Thomson expansion makes it a valuable tool in refrigeration.^[8] In vapor-compression refrigeration, as used in common refrigerators and air conditioners, it produces cooling in the throttling valve. The effect is applied in the Linde technique as a standard process in the petrochemical industry, where the cooling effect is used to liquefy gases, and also in many cryogenic applications (e.g. for the production of liquid oxygen, nitrogen, and argon). A gas must be below its inversion temperature to be liquefied by the Linde cycle. For this reason, simple Linde cycle liquefiers, starting from ambient temperature, cannot normally be used to liquefy helium, hydrogen, or neon. However, the Joule-Thomson effect can be used to liquefy even helium, provided that the helium gas is first cooled below its inversion temperature of 40 K.^[2]

The physical mechanism associated with the Joule–Thomson effect is closely related to that of a shock wave,^[9] although a shock wave differs in that the change in bulk kinetic energy of the gas flow is not negligible.

Physical mechanism (old version)

At low temperature, the Joule-Thomson coefficient of a gas is positive (the gas cools when it expands), at high temperature it is negative. This is a result of the way in which intermolecular forces affect both the energy and volume of the gas. Here we seek a physical understanding of why the temperature changes and why it sometimes warms and sometimes cools. Although microscopic concepts, such as interactions between molecules, are crucial to understanding this behavior, they are not entirely sufficient. This is because we are dealing with a process at constant enthalpy and enthalpy is a macroscopic quantity with no microscopic interpretation.

In an ideal gas, there are no intermolecular forces; but in real gases there are. The Joule–Thomson effect depends crucially on the deviation from ideal behavior produced by the attractive and the repulsive intermolecular forces (as illustrated, for example, by the Lennard-Jones potential). The attractive interactions act over a much longer range than the repulsive interactions. Since distances between molecules are large compared to the size of the molecules, the energy of a gas is influenced mainly by the attractive part of the potential (except at temperatures much higher than those considered here^[1]).

However, the repulsive part of the potential, which keeps two molecules from occupying the same space, can have a significant impact on the volume of the gas.

The internal energy is the sum of internal kinetic energy and internal potential energy. The internal kinetic energy is directly proportional to temperature, so by determining how it changes, we can determine how the temperature changes. As a gas expands, the average distance between molecules grows. Because of the attractive part of the intermolecular force, expansion causes an increase in the internal potential energy of the gas. Thus, if internal energy is kept constant, the internal kinetic energy must decrease and T must also decrease.

But the internal energy does not remain constant in a Joule-Thomson expansion; it is the enthalpy that remains constant. The enthalpy, $H$ , is defined as

H=U+PV

where $U$ is internal energy, $P$ is pressure, and $V$ is volume. Under the conditions of a Joule-Thomson expansion, the change in $PV$ represents the work done by the gas (see the proof below). If $PV$ increases, with $H$ constant, then $U$ must decrease as a result of the gas doing work on its surroundings. In this case, the internal kinetic energy decreases as a result of both the decrease in total internal energy and the conversion of some of the internal kinetic energy to internal potential energy. As a result, the temperature decreases and we have a positive Joule-Thomson coefficient.

For an ideal gas, $PV$ does not change during a Joule-Thomson expansion. As a result, there is no change in internal energy; since there is also no change in internal potential energy, there can be no change in internal kinetic energy and, therefore, no change in temperature. In real gases, $PV$ does change.

The ratio of the actual value of $PV$ to that expected for an ideal gas at the same temperature is called the compressibility factor, $Z$ . This is typically less than unity at low temperature and greater than unity at high temperature (see the discussion in compressibility factor). The value of $Z$ always moves towards unity as a gas expands. Thus at low temperature, $Z$ and $PV$ will increase as the gas expands. As a result, work is done on the surroundings, internal energy and temperature both decrease, and we have a positive Joule-Thomson coefficient. At high temperature, $Z$ and $PV$ decrease as the gas expands resulting in work being done on the gas. This results in an increase in temperature if the work done on the gas exceeds the increase in internal potential energy.

^ ^a ^b Goussard, J.-O.; Roulet, B. (1993). "Free expansion for real gases". Am. J. Phys. 61: 845–848.
^ ^a ^b Atkins, Peter (1997). Physical Chemistry (6th ed.). New York: W.H. Freeman and Co. p. 930. ISBN 0-7167-2871-0.
^ Rock, P. A. (1983). "Chemical Thermodynamics", section 3-2. University Science Books, Mill Valley, CA. ISBN0-935702-12-1
^ Pippard, A. B. (1957). "Elements of Classical Thermodynamics", p. 73. Cambridge University Press, Cambridge, U.K.
^ Tabor, D. (1991). Gases, liquids and solids, p. 148. Cambridge University Press, Cambridge, U.K. ISBN 0 521 40667 6.
^ Klotz, I.M. and R. M. Rosenberg (1991). Chemical Thermodynamics, p. 83. Benjamin, Meno Park, California.
^ ^a ^b Atkins, Peter (1997). Physical Chemistry (6th ed.). New York: W.H. Freeman and Co. pp. 31-32. ISBN 0-7167-2871-0.
^ Keenan, J.H. (1970). Thermodynamics, Chapter 15. M.I.T. Press, Cambridge, Massachusetts.
^ Hoover, Wm G., Carol G. Hoover, and Karl P. Travis. "Shock-Wave Compression and Joule-Thomson Expansion." Physical review letters 112.14 (2014): 144504. http://journals.aps.org/prl/abstract/10.1103/PhysRevLett.112.144504

[:Goussard-1] Goussard, J.-O.; Roulet, B. (1993). "Free expansion for real gases". Am. J. Phys. 61: 845–848.

[:Atkins1-2] Atkins, Peter (1997). Physical Chemistry (6th ed.). New York: W.H. Freeman and Co. p. 930. ISBN 0-7167-2871-0.

[:Rock-3] Rock, P. A. (1983). "Chemical Thermodynamics", section 3-2. University Science Books, Mill Valley, CA. ISBN0-935702-12-1

[:Pippard-4] Pippard, A. B. (1957). "Elements of Classical Thermodynamics", p. 73. Cambridge University Press, Cambridge, U.K.

[5] Tabor, D. (1991). Gases, liquids and solids, p. 148. Cambridge University Press, Cambridge, U.K. ISBN 0 521 40667 6.

[6] Klotz, I.M. and R. M. Rosenberg (1991). Chemical Thermodynamics, p. 83. Benjamin, Meno Park, California.

[:Atkins2-7] Atkins, Peter (1997). Physical Chemistry (6th ed.). New York: W.H. Freeman and Co. pp. 31-32. ISBN 0-7167-2871-0.

[8] Keenan, J.H. (1970). Thermodynamics, Chapter 15. M.I.T. Press, Cambridge, Massachusetts.

[9] Hoover, Wm G., Carol G. Hoover, and Karl P. Travis. "Shock-Wave Compression and Joule-Thomson Expansion." Physical review letters 112.14 (2014): 144504. http://journals.aps.org/prl/abstract/10.1103/PhysRevLett.112.144504

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]