Electrodynamic suspension

Jumping rings lift when an AC current energises a coil and the electrodynamic forces pushes the rings upwards against gravity

Electrodynamic suspension (EDS) is a form of magnetic levitation in which there are conductors which are exposed to time-varying magnetic fields. This induces eddy currents in the conductors that creates a repulsive magnetic field which holds the two objects apart.

These time varying magnetic fields can be caused by relative motion between two objects. In many cases, one magnetic field is a permanent field, such as a permanent magnet or a superconducting magnet, and the other magnetic field is induced from the changes of the field that occur as the magnet moves relative to a conductor in the other object.

Electrodynamic suspension can also occur when an electromagnet driven by an AC electrical source produces the changing magnetic field, in some cases, a linear induction motor generates the field.

EDS is used for maglev trains, such as the Japanese SCMaglev. It is also used for some classes of magnetically levitated bearings.

Types

Many examples of this have been used over the years.

Bedford levitator

In this early configuration by Bedford, Peer, and Tonks from 1939, an aluminum plate is placed on two concentric cylindrical coils, and driven with an AC current. When the parameters are correct, the plate exhibits 6-axis stable levitation.

Levitation melting

In the 1950s, a technique was developed where small quantities of metal were levitated and melted by a magnetic field of a few tens of kHz. The coil was a metal pipe, allowing coolant to be circulated through it. The overall form was generally conical, with a flat top. This permitted an inert atmosphere to be employed, and was commercially successful.

Linear induction motor

The field from a linear motor generates currents in an aluminum or copper sheet that creates lift forces as well as propulsion.

Main article: linear induction motor

Eric Laithwaite and colleagues took the Bedford levitator, and by stages developed and improved it.

First they made the levitator longer along one axis, and were able to make a levitator that was neutrally stable along one axis, and stable along all other axes.

Further development included replacing the single phase energising current with a linear induction motor which combined levitation and thrust.

Later "traverse-flux" systems at his Imperial College laboratory, such as Magnetic river avoided most of the problems of needing to have long, thick iron backing plates when having very long poles, by closing the flux path laterally by arranging the two opposite long poles side by side. They were also able to break the levitator primary into convenient sections which made it easier to build and transport.

Null flux

Null flux systems work by having coils that are exposed to a magnetic field, but are wound in figure of 8 and similar configurations such that when there is relative movement between the magnet and coils, but centered, no current flows since the potential cancels out. When they are displaced off-center, current flows and a strong field is generated by the coil which tends to restore the spacing.

These schemes were proposed by Powell and Danby in the 1960s, and they suggested that superconducting magnets could be used to generate the high magnetic pressure needed.

Inductrack

Main article: inductrack

Inductrack is a passive, fail-safe magnetic levitation system, using only unpowered loops of wire in the track and permanent magnets (arranged into Halbach arrays) on the vehicle to achieve magnetic levitation. The track can be in one of two configurations, a "ladder track" and a "laminated track". The ladder track is made of unpowered Litz wire cables, and the laminated track is made out of stacked copper or aluminium sheets.

There are two designs: the Inductrack I, which is optimized for high speed operation, and the Inductrack II, which is more efficient at lower speeds.

Electrodynamic bearing

3D-image of an axially magnetized ring magnet surrounded by a copper cylinder. The metal ring around the outside spins and the currents generated when it is off-center relative to the magnet push it back into alignment.

Main article: electrodynamic bearing

Electrodynamic bearings (EDB) are a novel type of bearing that is a passive magnetic technology. EDBs do not require any control electronics to operate. They work by the electrical currents generated by motion causing a restoring force.

Uses

Maglev

The JR Central SCMaglev train uses null flux superconductor magnet-based electrodynamic levitation.

In EDS maglev trains, both the rail and the train exert a magnetic field, and the train is levitated by the repulsive force between these magnetic fields. The magnetic field in the train is produced by either superconducting magnets (as in SCMaglev) or by an array of permanent magnets (as in Inductrack). The repulsive force in the track is created by an induced magnetic field in wires or other conducting strips in the track. A major advantage of the repulsive maglev systems is that they are naturally stable - minor narrowing in distance between the track and the magnets creates strong forces to repel the magnets back to their original position, while a slight increase in distance greatly reduces the force and again returns the vehicle to the right separation. No feedback control is necessarily needed.

Repulsive systems have a major downside as well. At slow speeds, the current induced in these coils by the slow change in magnetic flux with respect to time is not large enough to produce a repulsive electromagnetic force sufficient to support the weight of the train. Moreover, the energy efficiency for EDS at low speed is low. For this reason the train must have wheels or some other form of landing gear to support the train until it reaches a speed that can sustain levitation. Since a train may stop at any location, due to equipment problems for instance, the entire track must be able to support both low-speed and high-speed operation. Another downside is that the repulsive system naturally creates a field in the track in front and to the rear of the lift magnets, which act against the magnets and create a form of drag. This is generally only a concern at low speeds; at higher speeds the effect does not have time to build to its full potential and other forms of drag dominate.

The drag force can be used to the electrodynamic system's advantage, however, as it creates a varying force in the rails that can be used as a reactionary system to drive the train, without the need for a separate reaction plate, as in most linear motor systems.

Alternatively, propulsion coils on the guideway are used to exert a force on the magnets in the train and make the train move forward. The propulsion coils that exert a force on the train are effectively a linear motor: an alternating current flowing through the coils generates a continuously varying magnetic field that moves forward along the track. The frequency of the alternating current is synchronized to match the speed of the train. The offset between the field exerted by magnets on the train and the applied field creates a force moving the train forward.

Principles

Levitation and thrust force curves of a linear motor

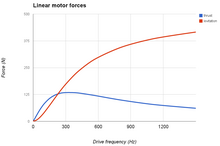
When a conductive loop experiences a changing magnetic field, from Lenz's law and Faraday's law, the changing magnetic field generates an Electromotive Force (EMF) around the circuit. For a sinusoidal excitation, this EMF is 90 degrees phased ahead of the field, peaking where the changes are most rapid (rather than when it is strongest):

${\mathcal {E}}=-N{{d\Phi _{B}} \over dt}$

where N is the number of turns of wire (for a simple loop this is 1) and Φ_B is the magnetic flux in webers through a single loop.

Since the field and potentials are out of phase, both attractive and repulsive forces are produced, and it might be expected that no net lift would be generated. However, although the EMF is at 90 degrees to the applied magnetic field, the loop inevitably has inductance. This inductive impedance tends to delay the peak current, by a phase angle dependent on the frequency (since the inductive impedance of any loop increases with frequency).

$K=R+i\omega L\,$

where K is impedance of the coil, L is the inductance and R is the resistance, the actual phase lead being derivable as the inverse tangent of the product ωL/R, viz., the standard phase lead evidence in a single-loop RL circuit.

But:

${\mathcal {E}}=IK$

where I is the current.

Thus at low frequencies, the phases are largely orthogonal and the currents lower, and no significant lift is generated. But at sufficiently high frequency, the inductive impedance dominates and the current and the applied field are virtually in line, and this current generates a magnetic field that is opposed to the applied one, and this permits levitation.

However, since the inductive impedance increases proportionally with frequency, so does the EMF, so the current tends to a limit when the resistance is small relative to the inductive impedance. This also limits the lift force. Power used for levitation is therefore largely constant with frequency. However, there are also eddy currents due to the finite size of conductors used in the coils, and these continue to grow with frequency.

Since the energy stored in the air gap can be calculated from HB/2 (or μ₀H²/2) times air-gap volume, the force applied across the air gap in the direction perpendicular to the load (viz., the force that directly counteracts gravity) is given by the spatial derivative (= gradient) of that energy. The air-gap volume equals the cross-sectional area multiplied by the width of the air gap, so the width cancels out and we are left with a suspensive force of μ₀H²/2 times air-gap cross-sectional area, which means that maximum bearable load varies as the square of the magnetic field density of the magnet, permanent or otherwise and varies directly as the cross-sectional area.

Stability

Static

Unlike configurations of simple permanent magnets, electrodynamic levitation can be made stable. Electrodynamic levitation with metallic conductors exhibits a form of diamagnetism, and relative permeabilities of around 0.7 can be achieved (depending on the frequency and conductor configuration). Given the details of the applicable hysteresis loop, frequency-dependent variability of behavior should be of minimal importance for those magnetic materials that are likely to be deployed.

Dynamic

This form of maglev can cause the levitated object to be subject to a drag induced oscillation, and this oscillation always occurs at a sufficiently high speed. These oscillations can be quite serious and can cause the suspension to fail.

However, inherent system level damping can frequently avoid this from occurring, particularly on large scale systems.

Alternatively, addition of lightweight tuned mass dampers can prevent oscillations from being problematic.

Electronic stabilization can also be employed.

See also

• Electromagnetic suspension
• Electrodynamic wheel
• Inductrack
• Suspension (mechanics)