Square root of 3
This article has an unclear citation style. (April 2024) |
 The height of an equilateral triangle with sides of length 2 equals the square root of 3. | |
| Representations | |
|---|---|
| Decimal | 1.7320508075688772935... |
| Continued fraction | |
The square root of 3 is the positive real number that, when multiplied by itself, gives the number 3. It is denoted mathematically as or . It is more precisely called the principal square root of 3 to distinguish it from the negative number with the same property. The square root of 3 is an irrational number. It is also known as Theodorus' constant, after Theodorus of Cyrene, who proved its irrationality.[citation needed]
In 2013, its numerical value in decimal notation was computed to ten billion digits.[1] Its decimal expansion, written here to 65 decimal places, is given by OEIS: A002194:
- 1.732050807568877293527446341505872366942805253810380628055806
The fraction (1.732142857...) can be used as a good approximation. Despite having a denominator of only 56, it differs from the correct value by less than (approximately , with a relative error of ). The rounded value of 1.732 is correct to within 0.01% of the actual value.[citation needed]
The fraction (1.73205080756...) is accurate to .[citation needed]
Archimedes reported a range for its value: .[2]
The lower limit is an accurate approximation for to (six decimal places, relative error ) and the upper limit to (four decimal places, relative error ).
Expressions
[edit]It can be expressed as the simple continued fraction [1; 1, 2, 1, 2, 1, 2, 1, …] (sequence A040001 in the OEIS).
So it is true to say:
then when :
Geometry and trigonometry
[edit]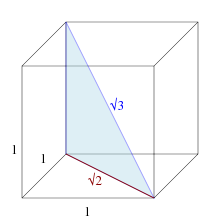


The square root of 3 can be found as the leg length of an equilateral triangle that encompasses a circle with a diameter of 1.
If an equilateral triangle with sides of length 1 is cut into two equal halves, by bisecting an internal angle across to make a right angle with one side, the right angle triangle's hypotenuse is length one, and the sides are of length and . From this, , , and .
The square root of 3 also appears in algebraic expressions for various other trigonometric constants, including[3] the sines of 3°, 12°, 15°, 21°, 24°, 33°, 39°, 48°, 51°, 57°, 66°, 69°, 75°, 78°, 84°, and 87°.
It is the distance between parallel sides of a regular hexagon with sides of length 1.
It is the length of the space diagonal of a unit cube.
The vesica piscis has a major axis to minor axis ratio equal to . This can be shown by constructing two equilateral triangles within it.
Other uses and occurrence
[edit]Power engineering
[edit]In power engineering, the voltage between two phases in a three-phase system equals times the line to neutral voltage. This is because any two phases are 120° apart, and two points on a circle 120 degrees apart are separated by times the radius (see geometry examples above).[citation needed]
Special functions
[edit]It is known that most roots of the nth derivatives of (where n < 18 and is the Bessel function of the first kind of order ) are transcendental. The only exceptions are the numbers , which are the algebraic roots of both and . [4][clarification needed]
References
[edit]- ^ Komsta, Łukasz (December 2013). "Computations | Łukasz Komsta". komsta.net. WordPress. Archived from the original on 2023-10-02. Retrieved September 24, 2016.
- ^ Knorr, Wilbur R. (June 1976). "Archimedes and the measurement of the circle: a new interpretation". Archive for History of Exact Sciences. 15 (2): 115–140. doi:10.1007/bf00348496. JSTOR 41133444. MR 0497462. S2CID 120954547. Retrieved November 15, 2022 – via SpringerLink.
- ^ Wiseman, Julian D. A. (June 2008). "Sin and Cos in Surds". JDAWiseman.com. Retrieved November 15, 2022.
- ^ Lorch, Lee; Muldoon, Martin E. (1995). "Transcendentality of zeros of higher dereivatives of functions involving Bessel functions". International Journal of Mathematics and Mathematical Sciences. 18 (3): 551–560. doi:10.1155/S0161171295000706.
- Podestá, Ricardo A. (2020). "A geometric proof that sqrt 3, sqrt 5, and sqrt 7 are irrational". arXiv:2003.06627 [math.GM].
Further reading
[edit]- The review of: Jones, M. F. (1968). "22900D approximations to the square roots of the primes less than 100". Mathematics of Computation. 22 (101): 234–235. doi:10.2307/2004806. JSTOR 2004806.
- Uhler, H. S. (1951). "Approximations exceeding 1300 decimals for , , and distribution of digits in them". Proc. Natl. Acad. Sci. U.S.A. 37 (7): 443–447. doi:10.1073/pnas.37.7.443. PMC 1063398. PMID 16578382.
- Wells, D. (1997). The Penguin Dictionary of Curious and Interesting Numbers (Revised ed.). London: Penguin Group. p. 23.
External links
[edit]- Theodorus' Constant at MathWorld
- Kevin Brown, Archimedes and the Square Root of 3





































