Dubins path
In geometry, the term Dubins path typically refers to the shortest curve that connects two points in the two-dimensional Euclidean plane (i.e. x-y plane) with a constraint on the curvature of the path and with prescribed initial and terminal tangents to the path, and an assumption that the vehicle traveling the path can only travel forward. If the vehicle can also travel in reverse, then the path follows the Reeds–Shepp curve.[1]
Lester Eli Dubins (1920–2010)[2] proved using tools from analysis[3] that any such path will consist of maximum curvature and/or straight line segments. In other words, the shortest path will be made by joining circular arcs of maximum curvature and straight lines.
Discussion
[edit]Dubins proved his result in 1957. In 1974 Harold H. Johnson proved Dubins' result by applying Pontryagin's maximum principle.[4] In particular, Harold H. Johnson presented necessary and sufficient conditions for a plane curve, which has bounded piecewise continuous curvature and prescribed initial and terminal points and directions, to have minimal length. In 1992 the same result was shown again using Pontryagin's maximum principle.[5] More recently, a geometric curve-theoretic proof has been provided by J. Ayala, D. Kirszenblat and J. Hyam Rubinstein.[6] A proof characterizing Dubins paths in homotopy classes has been given by J. Ayala.[7]
Applications
[edit]The Dubins path is commonly used in the fields of robotics and control theory as a way to plan paths for wheeled robots, airplanes and underwater vehicles. There are simple geometric[8] and analytical methods[9] to compute the optimal path.
For example, in the case of a wheeled robot, a simple kinematic car model (also known as Dubins' car) for the systems is: where is the car's position, is the heading, the car is moving at a constant speed , and the turn rate control is bounded. In this case the maximum turning rate corresponds to some minimum turning radius (and equivalently maximum curvature). The prescribed initial and terminal tangents correspond to initial and terminal headings. The Dubins' path gives the shortest path joining two oriented points that is feasible for the wheeled-robot model.
The optimal path type can be described using an analogy with cars of making a 'right turn (R)', 'left turn (L)' or driving 'straight (S).' An optimal path will always be at least one of the six types: RSR, RSL, LSR, LSL, RLR, LRL. For example, consider that for some given initial and final positions and tangents, the optimal path is shown to be of the type 'RSR.' Then this corresponds to a right-turn arc (R) followed by a straight line segment (S) followed by another right-turn arc (R). Moving along each segment in this sequence for the appropriate length will form the shortest curve that joins a starting point A to a terminal point B with the desired tangents at each endpoint and that does not exceed the given curvature.
-
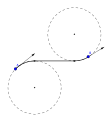
An RSL Dubins path
-
An RSR Dubins path
-
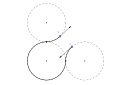
An LRL Dubins path
Dubins interval problem
[edit]Dubins interval problem is a key variant of the Dubins path problem, where an interval of heading directions are specified at the initial and terminal points. The tangent direction of the path at initial and final points are constrained to lie within the specified intervals. One could solve this using geometrical analysis,[10] or using Pontryagin's minimum principle.[11]
References
[edit]- ^ Reeds, J. A.; Shepp, L. A. (1990). "Optimal paths for a car that goes both forwards and backwards". Pacific Journal of Mathematics. 145 (2): 367–393. doi:10.2140/pjm.1990.145.367.
- ^ "IN MEMORIAM Lester Eli Dubins Professor of Mathematics and Statistics, Emeritus UC Berkeley 1920–2010". University of California. Archived from the original on 15 September 2011. Retrieved 26 May 2012.
- ^ Dubins, L. E. (July 1957). "On Curves of Minimal Length with a Constraint on Average Curvature, and with Prescribed Initial and Terminal Positions and Tangents". American Journal of Mathematics. 79 (3): 497–516. doi:10.2307/2372560. JSTOR 2372560.
- ^ Johnson, Harold H. (1974). "An application of the maximum principle to the geometry of plane curves". Proceedings of the American Mathematical Society. 44 (2): 432–435. doi:10.1090/S0002-9939-1974-0348631-6. MR 0348631.
- ^ Boissonat, J.-D.; Cerezo, A.; Leblond, K. (May 1992). "Shortest Paths of Bounded Curvature in the Plane" (PDF). Proceedings of the IEEE International Conference on Robotics and Automation. Vol. 3. Piscataway, NJ. pp. 2315–2320. doi:10.1109/ROBOT.1992.220117.
- ^ Ayala, José; Kirszenblat, David; Rubinstein, Hyam (2018). "A Geometric approach to shortest bounded curvature paths". Communications in Analysis and Geometry. 26 (4): 679–697. arXiv:1403.4899. doi:10.4310/CAG.2018.v26.n4.a1.
- ^ Ayala, José (2015). "Length minimising bounded curvature paths in homotopy classes". Topology and Its Applications. 193: 140–151. arXiv:1403.4930. doi:10.1016/j.topol.2015.06.008.
- ^ Anisi, David (July 2003). Optimal Motion Control of a Ground Vehicle (PDF) (Report). Swedish Research Defence Agency. 1650-1942.
- ^ Bui, Xuan-Nam; Boissonnat, J.-D.; Soueres, P.; Laumond, J.-P. (May 1994). "Shortest Path Synthesis for Dubins Non-Holonomic Robot". IEEE Conference on Robotics and Automation. Vol. 1. San Diego, CA. pp. 2–7. doi:10.1109/ROBOT.1994.351019.
- ^ Manyam, Satyanarayana; Rathinam, Sivakumar (2016). "On Tightly Bounding the Dubins Traveling Salesman's Optimum". Journal of Dynamic Systems, Measurement, and Control. 140 (7): 071013. arXiv:1506.08752. doi:10.1115/1.4039099. S2CID 16191780.
- ^ Manyam, Satyanarayana G.; Rathinam, Sivakumar; Casbeer, David; Garcia, Eloy (2017). "Tightly Bounding the Shortest Dubins Paths Through a Sequence of Points". Journal of Intelligent & Robotic Systems. 88 (2–4): 495–511. doi:10.1007/s10846-016-0459-4. S2CID 30943273.
External links
[edit]- Dubins Curves Archived 2016-03-22 at the Wayback Machine, from Planning Algorithms by Steven M. LaValle
- Isochrons for a Dubins Car, a demonstration from Wolfram Demonstrations Project
- An open-source Python Reeds-Shepp implementation, authored by Built Robotics