Michell structures
Michell structures are structures that are optimal based on the criteria defined by A.G.M. Michell in his frequently referenced 1904 paper.[1]
Michell states that “a frame (today called truss) (is optimal) attains the limit of economy of material possible in any frame-structure under the same applied forces, if the space occupied by it can be subjected to an appropriate small deformation, such that the strains in all the bars of the frame are increased by equal fractions of their lengths, not less than the fractional change of length of any element of the space.”
The above conclusion is based on the Maxwell load-path theorem:
Where is the tension value in any tension element of length , is the compression value in any compression element of length and is a constant value which is based on external loads applied to the structure.
Based on the Maxwell load-path theorem, reducing load path of tension members will reduce by the same value the load path of compression elements for a given set of external loads. Structure with minimum load path is one having minimum compliance (having minimum weighted deflection in the points of applied loads weighted by the values of these loads). In consequence Michell structures are minimum compliance trusses.
Special cases
[edit]1. All bars of a truss are subject to a load of the same sign (tension or compression).
Required volume of material is the same for all possible cases for a given set of loads. Michell defines minimum required volume of material to be:
Where is the allowable stress in the material.
2. Mixed tension and compression bars
More general case are frames which consist of bars that both before and after the appropriate deformation, form curves of orthogonal systems. A two-dimensional orthogonal system remains orthogonal after stretching one series of curves and compressing the other with equal strain if and only if the inclination between any two adjacent curves of the same series is constant throughout their length. This requirement results with the perpendicular series of curves to be either:
a) systems of tangents and involutes or
b) systems of intersecting logarithmic spirals.
Note that straight line or a circle are special cases of a logarithmic spiral.
Examples
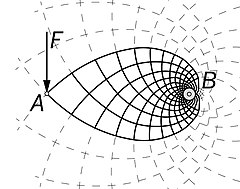
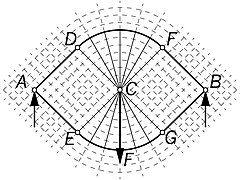
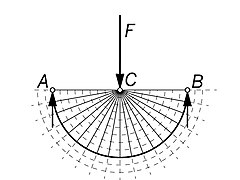
[edit]Michell provided several examples of optimum frames:
Prager trusses
[edit]In recent years a lot of studies have been done on discrete optimum trusses.[2][3][4] In spite of Michell trusses being defined for continuum (infinite number of members) these are sometimes called Michell trusses as well. Significant contribution to the topic of discrete optimum trusses had William Prager who used the method of the circle of relative displacements to arrive with optimal topology of such trusses (typically cantilevers). To recognize Prager's contribution discrete Michell trusses are sometimes called Prager trusses. Later geometry of cantilevered Prager trusses has been formalized by Mazurek, Baker and Tort [5][6] who noticed certain geometrical relationships between members of optimal discrete trusses for 3 point or 3 force problems.
References
[edit]- ^ Michell, A. G. M. (1904) The limits of economy of material in frame-structures, Philosophical Magazine, Vol. 8(47), p. 589-597.
- ^ Prager W., A Note on Discretized Michell Structures, Computer Methods in Applied Mechanics and Engineering, Vol. 3, pp. 349-355, 1974
- ^ Prager W. Optimal layout of cantilever trusses, Journal of Optimization Theory and Applications (1977) 23: 111. https://doi.org/10.1007/BF00932301
- ^ Prager W. Nearly optimal design of trusses, Computers & Structures, ISSN 0045-7949, Vol: 8, Issue: 3, Page: 451-454, 1978
- ^ Mazurek, A., Baker W.F. & Tort, C., Geometrical aspects of optimum truss like structures, Structural and Multidisciplinary Optimization (2011) 43: 231. https://doi.org/10.1007/s00158-010-0559-x
- ^ Mazurek, A., Geometrical aspects of optimum truss like structures for three-force problem, Structural and Multidisciplinary Optimization (2012) 45: 21. https://doi.org/10.1007/s00158-011-0679-y