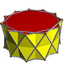
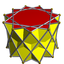
Hendecagrammic prism
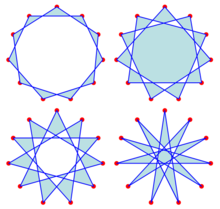
{11/2}, {11/3}, {11/4}, and {11/5}
In geometry, a hendecagrammic prism is a star polyhedron made from two identical regular hendecagrams connected by squares. The related hendecagrammic antiprisms are made from two identical regular hendecagrams connected by equilateral triangles.
Hendecagrammic prisms and bipyramids
[edit]There are 4 hendecagrammic uniform prisms, and 6 hendecagrammic uniform antiprisms. The prisms are constructed by 4.4.11/q vertex figures, 
Coxeter diagram. The hendecagrammic bipyramids, duals to the hendecagrammic prisms are also given.
| Symmetry | Prisms | |||
|---|---|---|---|---|
| D11h [2,11] (*2.2.11) |
 4.4.11/2 
|
 4.4.11/3 
|
 4.4.11/4 
|
 4.4.11/5 
|
| D11h [2,11] (*2.2.11) |
  
|
 
|
 
|
 
|
Hendecagrammic antiprisms
[edit]The antiprisms with 3.3.3.3.11/q vertex figures, 
. Uniform antiprisms exist for p/q>3/2,[1] and are called crossed for p/q<2. For hendecagonal antiprism, two crossed antiprisms can not be constructed as uniform (with equilateral triangles): 11/8, and 11/9.
| Symmetry | Antiprisms | Crossed- antiprisms | ||
|---|---|---|---|---|
| D11h [2,11] (*2.2.11) |
 3.3.3.11/2
|
 3.3.3.11/4
|
 3.3.3.11/6 3.3.3.-11/5 
|
Nonuniform 3.3.3.11/8 3.3.3.-11/3 |
| D11d [2+,11] (2*11) |
 3.3.3.11/3
|
 3.3.3.11/5
|
 3.3.3.11/7 3.3.3.-11/4 
|
Nonuniform 3.3.3.11/9 3.3.3.-11/2 |
Hendecagrammic trapezohedra
[edit]The hendecagrammic trapezohedra are duals to the hendecagrammic antiprisms.
| Symmetry | Trapezohedra | ||
|---|---|---|---|
| D11h [2,11] (*2.2.11) |
 
|
|
|
| D11d [2+,11] (2*11) |
|
|
 
|
See also
[edit]References
[edit]- ^ Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79 (3): 447–457, Bibcode:1976MPCPS..79..447S, doi:10.1017/S0305004100052440, MR 0397554.
- Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954). "Uniform polyhedra". Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. 246 (916). The Royal Society: 401–450. Bibcode:1954RSPTA.246..401C. doi:10.1098/rsta.1954.0003. ISSN 0080-4614. JSTOR 91532. MR 0062446. S2CID 202575183.