Great rhombidodecahedron
Appearance
(Redirected from Gird (geometry))
| Great rhombidodecahedron | |
|---|---|
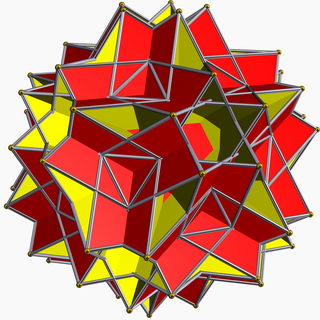
| |
| Type | Uniform star polyhedron |
| Elements | F = 42, E = 120 V = 60 (χ = −18) |
| Faces by sides | 30{4}+12{10/3} |
| Coxeter diagram | |
| Wythoff symbol | 2 5/3 (3/2 5/4) | |
| Symmetry group | Ih, [5,3], *532 |
| Index references | U73, C89, W109 |
| Dual polyhedron | Great rhombidodecacron |
| Vertex figure |  4.10/3.4/3.10/7 |
| Bowers acronym | Gird |

In geometry, the great rhombidodecahedron is a nonconvex uniform polyhedron, indexed as U73. It has 42 faces (30 squares, 12 decagrams), 120 edges and 60 vertices.[1] Its vertex figure is a crossed quadrilateral.
Related polyhedra
[edit]It shares its vertex arrangement with the truncated great dodecahedron and the uniform compounds of 6 or 12 pentagonal prisms. It additionally shares its edge arrangement with the nonconvex great rhombicosidodecahedron (having the square faces in common), and with the great dodecicosidodecahedron (having the decagrammic faces in common).
 Nonconvex great rhombicosidodecahedron |
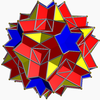 Great dodecicosidodecahedron |
 Great rhombidodecahedron |
 Truncated great dodecahedron |
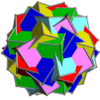 Compound of six pentagonal prisms |
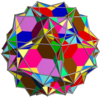 Compound of twelve pentagonal prisms |
Gallery
[edit] Traditional filling |
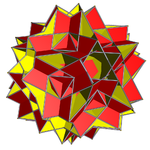 Modulo-2 filling |
See also
[edit]References
[edit]- ^ Maeder, Roman. "73: great rhombidodecahedron". MathConsult.
