Ratio of the perimeter of Bernoulli's lemniscate to its diameter
Lemniscate of Bernoulli In mathematics , the lemniscate constant ϖ is a transcendental mathematical constant that is the ratio of the perimeter of Bernoulli's lemniscate to its diameter , analogous to the definition of π [ 1]
(
x
2
+
y
2
)
2
=
x
2
−
y
2
{\displaystyle (x^{2}+y^{2})^{2}=x^{2}-y^{2}}
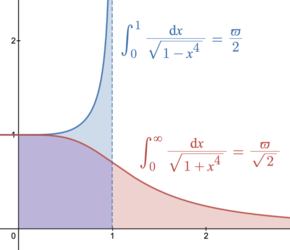
2ϖ . The lemniscate constant is closely related to the lemniscate elliptic functions and approximately equal to 2.62205755.[ 2] gamma and beta function at certain rational values. The symbol ϖ is a cursive variant of π ; see Pi § Variant pi .
Sometimes the quantities 2ϖ or ϖ/2 the lemniscate constant.[ 3] [ 4]
As of 2024 over 1.2 trillion digits of this constant have been calculated.[ 5]
Gauss's constant , denoted by G , is equal to ϖ /π ≈ 0.8346268[ 6] Carl Friedrich Gauss , who calculated it via the arithmetic–geometric mean as
1
/
M
(
1
,
2
)
{\displaystyle 1/M{\bigl (}1,{\sqrt {2}}{\bigr )}}
M
(
1
,
2
)
=
π
/
ϖ
{\displaystyle M{\bigl (}1,{\sqrt {2}}{\bigr )}=\pi /\varpi }
ϖ
{\displaystyle \varpi }
[ 8]
John Todd named two more lemniscate constants, the first lemniscate constant A = ϖ /2 ≈ 1.3110287771second lemniscate constant B = π /(2ϖ ) ≈ 0.5990701173[ 9] [ 10] [ 11]
The lemniscate constant
ϖ
{\displaystyle \varpi }
A
{\displaystyle A}
transcendental by Carl Ludwig Siegel in 1932 and later by Theodor Schneider in 1937 and Todd's second lemniscate constant
B
{\displaystyle B}
G
{\displaystyle G}
[ 9] [ 12] [ 13] Gregory Chudnovsky proved that the set
{
π
,
ϖ
}
{\displaystyle \{\pi ,\varpi \}}
algebraically independent over
Q
{\displaystyle \mathbb {Q} }
A
{\displaystyle A}
B
{\displaystyle B}
[ 14] [ 15]
{
π
,
M
(
1
,
1
/
2
)
,
M
′
(
1
,
1
/
2
)
}
{\displaystyle {\bigl \{}\pi ,M{\bigl (}1,1/{\sqrt {2}}{\bigr )},M'{\bigl (}1,1/{\sqrt {2}}{\bigr )}{\bigr \}}}
derivative with respect to the second variable) is not algebraically independent over
Q
{\displaystyle \mathbb {Q} }
[ 16] Yuri Nesterenko proved that the set
{
π
,
ϖ
,
e
π
}
{\displaystyle \{\pi ,\varpi ,e^{\pi }\}}
Q
{\displaystyle \mathbb {Q} }
[ 17]
Usually,
ϖ
{\displaystyle \varpi }
[ 18]
ϖ
=
2
∫
0
1
d
t
1
−
t
4
=
2
∫
0
∞
d
t
1
+
t
4
=
∫
0
1
d
t
t
−
t
3
=
∫
1
∞
d
t
t
3
−
t
=
4
∫
0
∞
(
1
+
t
4
4
−
t
)
d
t
=
2
2
∫
0
1
1
−
t
4
4
d
t
=
3
∫
0
1
1
−
t
4
d
t
=
2
K
(
i
)
=
1
2
B
(
1
4
,
1
2
)
=
1
2
2
B
(
1
4
,
1
4
)
=
Γ
(
1
/
4
)
2
2
2
π
=
2
−
2
4
ζ
(
3
/
4
)
2
ζ
(
1
/
4
)
2
=
2.62205
75542
92119
81046
48395
89891
11941
…
,
{\displaystyle {\begin{aligned}\varpi &=2\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}={\sqrt {2}}\int _{0}^{\infty }{\frac {\mathrm {d} t}{\sqrt {1+t^{4}}}}=\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {t-t^{3}}}}=\int _{1}^{\infty }{\frac {\mathrm {d} t}{\sqrt {t^{3}-t}}}\\[6mu]&=4\int _{0}^{\infty }{\Bigl (}{\sqrt[{4}]{1+t^{4}}}-t{\Bigr )}\,\mathrm {d} t=2{\sqrt {2}}\int _{0}^{1}{\sqrt[{4}]{1-t^{4}}}\mathop {\mathrm {d} t} =3\int _{0}^{1}{\sqrt {1-t^{4}}}\,\mathrm {d} t\\[2mu]&=2K(i)={\tfrac {1}{2}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )}={\tfrac {1}{2{\sqrt {2}}}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{4}}{\bigr )}={\frac {\Gamma (1/4)^{2}}{2{\sqrt {2\pi }}}}={\frac {2-{\sqrt {2}}}{4}}{\frac {\zeta (3/4)^{2}}{\zeta (1/4)^{2}}}\\[5mu]&=2.62205\;75542\;92119\;81046\;48395\;89891\;11941\ldots ,\end{aligned}}}
where K is the complete elliptic integral of the first kind with modulus k , Β is the beta function , Γ is the gamma function and ζ is the Riemann zeta function .
The lemniscate constant can also be computed by the arithmetic–geometric mean
M
{\displaystyle M}
ϖ
=
π
M
(
1
,
2
)
.
{\displaystyle \varpi ={\frac {\pi }{M{\bigl (}1,{\sqrt {2}}{\bigr )}}}.}
Gauss's constant is typically defined as the reciprocal of the arithmetic–geometric mean of 1 and the square root of 2 , after his calculation of
M
(
1
,
2
)
{\displaystyle M{\bigl (}1,{\sqrt {2}}{\bigr )}}
G
=
1
M
(
1
,
2
)
{\displaystyle G={\frac {1}{M{\bigl (}1,{\sqrt {2}}{\bigr )}}}}
beta function B:
A
=
ϖ
2
=
1
4
B
(
1
4
,
1
2
)
,
B
=
π
2
ϖ
=
1
4
B
(
1
2
,
3
4
)
.
{\displaystyle {\begin{aligned}A&={\frac {\varpi }{2}}={\tfrac {1}{4}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )},\\[3mu]B&={\frac {\pi }{2\varpi }}={\tfrac {1}{4}}\mathrm {B} {\bigl (}{\tfrac {1}{2}},{\tfrac {3}{4}}{\bigr )}.\end{aligned}}}
As a special value of L-functions [ edit ]
β
′
(
0
)
=
log
ϖ
π
{\displaystyle \beta '(0)=\log {\frac {\varpi }{\sqrt {\pi }}}}
which is analogous to
ζ
′
(
0
)
=
log
1
2
π
{\displaystyle \zeta '(0)=\log {\frac {1}{\sqrt {2\pi }}}}
where
β
{\displaystyle \beta }
Dirichlet beta function and
ζ
{\displaystyle \zeta }
Riemann zeta function .[ 20]
Analogously to the Leibniz formula for π ,
β
(
1
)
=
∑
n
=
1
∞
χ
(
n
)
n
=
π
4
,
{\displaystyle \beta (1)=\sum _{n=1}^{\infty }{\frac {\chi (n)}{n}}={\frac {\pi }{4}},}
[ 21] [ 22] [ 23] [ 24] [ 25]
L
(
E
,
1
)
=
∑
n
=
1
∞
ν
(
n
)
n
=
ϖ
4
{\displaystyle L(E,1)=\sum _{n=1}^{\infty }{\frac {\nu (n)}{n}}={\frac {\varpi }{4}}}
L
{\displaystyle L}
L-function of the elliptic curve
E
:
y
2
=
x
3
−
x
{\displaystyle E:\,y^{2}=x^{3}-x}
Q
{\displaystyle \mathbb {Q} }
ν
{\displaystyle \nu }
multiplicative function given by
ν
(
p
n
)
=
{
p
−
N
p
,
p
∈
P
,
n
=
1
0
,
p
=
2
,
n
≥
2
ν
(
p
)
ν
(
p
n
−
1
)
−
p
ν
(
p
n
−
2
)
,
p
∈
P
∖
{
2
}
,
n
≥
2
{\displaystyle \nu (p^{n})={\begin{cases}p-{\mathcal {N}}_{p},&p\in \mathbb {P} ,\,n=1\\[5mu]0,&p=2,\,n\geq 2\\[5mu]\nu (p)\nu (p^{n-1})-p\nu (p^{n-2}),&p\in \mathbb {P} \setminus \{2\},\,n\geq 2\end{cases}}}
N
p
{\displaystyle {\mathcal {N}}_{p}}
a
3
−
a
≡
b
2
(
mod
p
)
,
p
∈
P
{\displaystyle a^{3}-a\equiv b^{2}\,(\operatorname {mod} p),\quad p\in \mathbb {P} }
a
,
b
{\displaystyle a,b}
P
{\displaystyle \mathbb {P} }
ν
{\displaystyle \nu }
F
(
τ
)
=
η
(
4
τ
)
2
η
(
8
τ
)
2
=
∑
n
=
1
∞
ν
(
n
)
q
n
,
q
=
e
2
π
i
τ
{\displaystyle F(\tau )=\eta (4\tau )^{2}\eta (8\tau )^{2}=\sum _{n=1}^{\infty }\nu (n)q^{n},\quad q=e^{2\pi i\tau }}
τ
∈
C
{\displaystyle \tau \in \mathbb {C} }
ℑ
τ
>
0
{\displaystyle \operatorname {\Im } \tau >0}
η
{\displaystyle \eta }
eta function .[ 26] [ 27] [ 28]
∑
n
=
1
∞
ν
(
n
)
n
e
−
2
π
n
/
32
=
ϖ
8
{\displaystyle \sum _{n=1}^{\infty }{\frac {\nu (n)}{n}}e^{-2\pi n/{\sqrt {32}}}={\frac {\varpi }{8}}}
32
{\displaystyle 32}
conductor of
E
{\displaystyle E}
BSD conjecture is true for the above
E
{\displaystyle E}
[ 29]
ν
{\displaystyle \nu }
1
≤
n
≤
113
{\displaystyle 1\leq n\leq 113}
n
{\displaystyle n}
ν
(
n
)
=
0
{\displaystyle \nu (n)=0}
n
ν
(
n
)
n
ν
(
n
)
1
1
53
14
5
−
2
61
−
10
9
−
3
65
−
12
13
6
73
−
6
17
2
81
9
25
−
1
85
−
4
29
−
10
89
10
37
−
2
97
18
41
10
101
−
2
45
6
109
6
49
−
7
113
−
14
{\displaystyle {\begin{array}{|c|c|c|c|}\hline n&\nu (n)&n&\nu (n)\\\hline 1&1&53&14\\\hline 5&-2&61&-10\\\hline 9&-3&65&-12\\\hline 13&6&73&-6\\\hline 17&2&81&9\\\hline 25&-1&85&-4\\\hline 29&-10&89&10\\\hline 37&-2&97&18\\\hline 41&10&101&-2\\\hline 45&6&109&6\\\hline 49&-7&113&-14\\\hline \end{array}}}
As a special value of other functions [ edit ] Let
Δ
{\displaystyle \Delta }
1
{\displaystyle 1}
[ 30]
Δ
(
i
)
=
1
64
(
ϖ
π
)
12
.
{\displaystyle \Delta (i)={\frac {1}{64}}\left({\frac {\varpi }{\pi }}\right)^{12}.}
q
{\displaystyle q}
Δ
{\displaystyle \Delta }
Ramanujan tau function .
Viète's formula for π can be written:
2
π
=
1
2
⋅
1
2
+
1
2
1
2
⋅
1
2
+
1
2
1
2
+
1
2
1
2
⋯
{\displaystyle {\frac {2}{\pi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}}}\cdots }
An analogous formula for ϖ is:[ 31]
2
ϖ
=
1
2
⋅
1
2
+
1
2
/
1
2
⋅
1
2
+
1
2
/
1
2
+
1
2
/
1
2
⋯
{\displaystyle {\frac {2}{\varpi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\bigg /}\!{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\Bigg /}\!{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\bigg /}\!{\sqrt {\frac {1}{2}}}}}}}\cdots }
The Wallis product for π is:
π
2
=
∏
n
=
1
∞
(
1
+
1
n
)
(
−
1
)
n
+
1
=
∏
n
=
1
∞
(
2
n
2
n
−
1
⋅
2
n
2
n
+
1
)
=
(
2
1
⋅
2
3
)
(
4
3
⋅
4
5
)
(
6
5
⋅
6
7
)
⋯
{\displaystyle {\frac {\pi }{2}}=\prod _{n=1}^{\infty }\left(1+{\frac {1}{n}}\right)^{(-1)^{n+1}}=\prod _{n=1}^{\infty }\left({\frac {2n}{2n-1}}\cdot {\frac {2n}{2n+1}}\right)={\biggl (}{\frac {2}{1}}\cdot {\frac {2}{3}}{\biggr )}{\biggl (}{\frac {4}{3}}\cdot {\frac {4}{5}}{\biggr )}{\biggl (}{\frac {6}{5}}\cdot {\frac {6}{7}}{\biggr )}\cdots }
An analogous formula for ϖ is:[ 32]
ϖ
2
=
∏
n
=
1
∞
(
1
+
1
2
n
)
(
−
1
)
n
+
1
=
∏
n
=
1
∞
(
4
n
−
1
4
n
−
2
⋅
4
n
4
n
+
1
)
=
(
3
2
⋅
4
5
)
(
7
6
⋅
8
9
)
(
11
10
⋅
12
13
)
⋯
{\displaystyle {\frac {\varpi }{2}}=\prod _{n=1}^{\infty }\left(1+{\frac {1}{2n}}\right)^{(-1)^{n+1}}=\prod _{n=1}^{\infty }\left({\frac {4n-1}{4n-2}}\cdot {\frac {4n}{4n+1}}\right)={\biggl (}{\frac {3}{2}}\cdot {\frac {4}{5}}{\biggr )}{\biggl (}{\frac {7}{6}}\cdot {\frac {8}{9}}{\biggr )}{\biggl (}{\frac {11}{10}}\cdot {\frac {12}{13}}{\biggr )}\cdots }
A related result for Gauss's constant (
G
=
ϖ
/
π
{\displaystyle G=\varpi /\pi }
[ 33]
ϖ
π
=
∏
n
=
1
∞
(
4
n
−
1
4
n
⋅
4
n
+
2
4
n
+
1
)
=
(
3
4
⋅
6
5
)
(
7
8
⋅
10
9
)
(
11
12
⋅
14
13
)
⋯
{\displaystyle {\frac {\varpi }{\pi }}=\prod _{n=1}^{\infty }\left({\frac {4n-1}{4n}}\cdot {\frac {4n+2}{4n+1}}\right)={\biggl (}{\frac {3}{4}}\cdot {\frac {6}{5}}{\biggr )}{\biggl (}{\frac {7}{8}}\cdot {\frac {10}{9}}{\biggr )}{\biggl (}{\frac {11}{12}}\cdot {\frac {14}{13}}{\biggr )}\cdots }
An infinite series discovered by Gauss is:[ 34]
ϖ
π
=
∑
n
=
0
∞
(
−
1
)
n
∏
k
=
1
n
(
2
k
−
1
)
2
(
2
k
)
2
=
1
−
1
2
2
2
+
1
2
⋅
3
2
2
2
⋅
4
2
−
1
2
⋅
3
2
⋅
5
2
2
2
⋅
4
2
⋅
6
2
+
⋯
{\displaystyle {\frac {\varpi }{\pi }}=\sum _{n=0}^{\infty }(-1)^{n}\prod _{k=1}^{n}{\frac {(2k-1)^{2}}{(2k)^{2}}}=1-{\frac {1^{2}}{2^{2}}}+{\frac {1^{2}\cdot 3^{2}}{2^{2}\cdot 4^{2}}}-{\frac {1^{2}\cdot 3^{2}\cdot 5^{2}}{2^{2}\cdot 4^{2}\cdot 6^{2}}}+\cdots }
The Machin formula for π is
1
4
π
=
4
arctan
1
5
−
arctan
1
239
,
{\textstyle {\tfrac {1}{4}}\pi =4\arctan {\tfrac {1}{5}}-\arctan {\tfrac {1}{239}},}
π can be developed using trigonometric angle sum identities, e.g. Euler's formula
1
4
π
=
arctan
1
2
+
arctan
1
3
{\textstyle {\tfrac {1}{4}}\pi =\arctan {\tfrac {1}{2}}+\arctan {\tfrac {1}{3}}}
ϖ , including the following found by Gauss:
1
2
ϖ
=
2
arcsl
1
2
+
arcsl
7
23
{\displaystyle {\tfrac {1}{2}}\varpi =2\operatorname {arcsl} {\tfrac {1}{2}}+\operatorname {arcsl} {\tfrac {7}{23}}}
arcsl
{\displaystyle \operatorname {arcsl} }
lemniscate arcsine .[ 35]
The lemniscate constant can be rapidly computed by the series[ 36] [ 37]
ϖ
=
2
−
1
/
2
π
(
∑
n
∈
Z
e
−
π
n
2
)
2
=
2
1
/
4
π
e
−
π
/
12
(
∑
n
∈
Z
(
−
1
)
n
e
−
π
p
n
)
2
{\displaystyle \varpi =2^{-1/2}\pi {\biggl (}\sum _{n\in \mathbb {Z} }e^{-\pi n^{2}}{\biggr )}^{2}=2^{1/4}\pi e^{-\pi /12}{\biggl (}\sum _{n\in \mathbb {Z} }(-1)^{n}e^{-\pi p_{n}}{\biggr )}^{2}}
where
p
n
=
1
2
(
3
n
2
−
n
)
{\displaystyle p_{n}={\tfrac {1}{2}}(3n^{2}-n)}
generalized pentagonal numbers ). Also[ 38]
∑
m
,
n
∈
Z
e
−
2
π
(
m
2
+
m
n
+
n
2
)
=
1
+
3
ϖ
12
1
/
8
π
.
{\displaystyle \sum _{m,n\in \mathbb {Z} }e^{-2\pi (m^{2}+mn+n^{2})}={\sqrt {1+{\sqrt {3}}}}{\dfrac {\varpi }{12^{1/8}\pi }}.}
In a spirit similar to that of the Basel problem ,
∑
z
∈
Z
[
i
]
∖
{
0
}
1
z
4
=
G
4
(
i
)
=
ϖ
4
15
{\displaystyle \sum _{z\in \mathbb {Z} [i]\setminus \{0\}}{\frac {1}{z^{4}}}=G_{4}(i)={\frac {\varpi ^{4}}{15}}}
where
Z
[
i
]
{\displaystyle \mathbb {Z} [i]}
Gaussian integers and
G
4
{\displaystyle G_{4}}
Eisenstein series of weight
4
{\displaystyle 4}
(see Lemniscate elliptic functions § Hurwitz numbers for a more general result).[ 39]
A related result is
∑
n
=
1
∞
σ
3
(
n
)
e
−
2
π
n
=
ϖ
4
80
π
4
−
1
240
{\displaystyle \sum _{n=1}^{\infty }\sigma _{3}(n)e^{-2\pi n}={\frac {\varpi ^{4}}{80\pi ^{4}}}-{\frac {1}{240}}}
where
σ
3
{\displaystyle \sigma _{3}}
sum of positive divisors function .[ 40]
In 1842, Malmsten found
β
′
(
1
)
=
∑
n
=
1
∞
(
−
1
)
n
+
1
log
(
2
n
+
1
)
2
n
+
1
=
π
4
(
γ
+
2
log
π
ϖ
2
)
{\displaystyle \beta '(1)=\sum _{n=1}^{\infty }(-1)^{n+1}{\frac {\log(2n+1)}{2n+1}}={\frac {\pi }{4}}\left(\gamma +2\log {\frac {\pi }{\varpi {\sqrt {2}}}}\right)}
where
γ
{\displaystyle \gamma }
Euler's constant and
β
(
s
)
{\displaystyle \beta (s)}
The lemniscate constant is given by the rapidly converging series
ϖ
=
π
32
4
e
−
π
3
(
∑
n
=
−
∞
∞
(
−
1
)
n
e
−
2
n
π
(
3
n
+
1
)
)
2
.
{\displaystyle \varpi =\pi {\sqrt[{4}]{32}}e^{-{\frac {\pi }{3}}}{\biggl (}\sum _{n=-\infty }^{\infty }(-1)^{n}e^{-2n\pi (3n+1)}{\biggr )}^{2}.}
The constant is also given by the infinite product
ϖ
=
π
∏
m
=
1
∞
tanh
2
(
π
m
2
)
.
{\displaystyle \varpi =\pi \prod _{m=1}^{\infty }\tanh ^{2}\left({\frac {\pi m}{2}}\right).}
Also[ 41]
∑
n
=
0
∞
(
−
1
)
n
6635520
n
(
4
n
)
!
n
!
4
=
24
5
7
/
4
ϖ
2
π
2
.
{\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{6635520^{n}}}{\frac {(4n)!}{n!^{4}}}={\frac {24}{5^{7/4}}}{\frac {\varpi ^{2}}{\pi ^{2}}}.}
Continued fractions [ edit ] A (generalized) continued fraction for π is
π
2
=
1
+
1
1
+
1
⋅
2
1
+
2
⋅
3
1
+
3
⋅
4
1
+
⋱
{\displaystyle {\frac {\pi }{2}}=1+{\cfrac {1}{1+{\cfrac {1\cdot 2}{1+{\cfrac {2\cdot 3}{1+{\cfrac {3\cdot 4}{1+\ddots }}}}}}}}}
ϖ is[ 10]
ϖ
2
=
1
+
1
2
+
2
⋅
3
2
+
4
⋅
5
2
+
6
⋅
7
2
+
⋱
{\displaystyle {\frac {\varpi }{2}}=1+{\cfrac {1}{2+{\cfrac {2\cdot 3}{2+{\cfrac {4\cdot 5}{2+{\cfrac {6\cdot 7}{2+\ddots }}}}}}}}}
Define Brouncker 's continued fraction[ 42]
b
(
s
)
=
s
+
1
2
2
s
+
3
2
2
s
+
5
2
2
s
+
⋱
,
s
>
0.
{\displaystyle b(s)=s+{\cfrac {1^{2}}{2s+{\cfrac {3^{2}}{2s+{\cfrac {5^{2}}{2s+\ddots }}}}}},\quad s>0.}
n
≥
0
{\displaystyle n\geq 0}
n
≥
1
{\displaystyle n\geq 1}
[ 43] [ 44]
b
(
4
n
)
=
(
4
n
+
1
)
∏
k
=
1
n
(
4
k
−
1
)
2
(
4
k
−
3
)
(
4
k
+
1
)
π
ϖ
2
b
(
4
n
+
1
)
=
(
2
n
+
1
)
∏
k
=
1
n
(
2
k
)
2
(
2
k
−
1
)
(
2
k
+
1
)
4
π
b
(
4
n
+
2
)
=
(
4
n
+
1
)
∏
k
=
1
n
(
4
k
−
3
)
(
4
k
+
1
)
(
4
k
−
1
)
2
ϖ
2
π
b
(
4
n
+
3
)
=
(
2
n
+
1
)
∏
k
=
1
n
(
2
k
−
1
)
(
2
k
+
1
)
(
2
k
)
2
π
.
{\displaystyle {\begin{aligned}b(4n)&=(4n+1)\prod _{k=1}^{n}{\frac {(4k-1)^{2}}{(4k-3)(4k+1)}}{\frac {\pi }{\varpi ^{2}}}\\b(4n+1)&=(2n+1)\prod _{k=1}^{n}{\frac {(2k)^{2}}{(2k-1)(2k+1)}}{\frac {4}{\pi }}\\b(4n+2)&=(4n+1)\prod _{k=1}^{n}{\frac {(4k-3)(4k+1)}{(4k-1)^{2}}}{\frac {\varpi ^{2}}{\pi }}\\b(4n+3)&=(2n+1)\prod _{k=1}^{n}{\frac {(2k-1)(2k+1)}{(2k)^{2}}}\,\pi .\end{aligned}}}
b
(
1
)
=
4
π
,
b
(
2
)
=
ϖ
2
π
,
b
(
3
)
=
π
,
b
(
4
)
=
9
π
ϖ
2
.
{\displaystyle {\begin{aligned}b(1)&={\frac {4}{\pi }},&b(2)&={\frac {\varpi ^{2}}{\pi }},&b(3)&=\pi ,&b(4)&={\frac {9\pi }{\varpi ^{2}}}.\end{aligned}}}
In fact, the values of
b
(
1
)
{\displaystyle b(1)}
b
(
2
)
{\displaystyle b(2)}
b
(
s
+
2
)
=
(
s
+
1
)
2
b
(
s
)
,
{\displaystyle b(s+2)={\frac {(s+1)^{2}}{b(s)}},}
b
(
n
)
{\displaystyle b(n)}
n
{\displaystyle n}
Simple continued fractions [ edit ] Simple continued fractions for the lemniscate constant and related constants include[ 45] [ 46]
ϖ
=
[
2
,
1
,
1
,
1
,
1
,
1
,
4
,
1
,
2
,
…
]
,
2
ϖ
=
[
5
,
4
,
10
,
2
,
1
,
2
,
3
,
29
,
…
]
,
ϖ
2
=
[
1
,
3
,
4
,
1
,
1
,
1
,
5
,
2
,
…
]
,
ϖ
π
=
[
0
,
1
,
5
,
21
,
3
,
4
,
14
,
…
]
.
{\displaystyle {\begin{aligned}\varpi &=[2,1,1,1,1,1,4,1,2,\ldots ],\\[8mu]2\varpi &=[5,4,10,2,1,2,3,29,\ldots ],\\[5mu]{\frac {\varpi }{2}}&=[1,3,4,1,1,1,5,2,\ldots ],\\[2mu]{\frac {\varpi }{\pi }}&=[0,1,5,21,3,4,14,\ldots ].\end{aligned}}}
A geometric representation of
ϖ
/
2
{\displaystyle \varpi /2}
ϖ
/
2
{\displaystyle \varpi /{\sqrt {2}}}
The lemniscate constant ϖ is related to the area under the curve
x
4
+
y
4
=
1
{\displaystyle x^{4}+y^{4}=1}
π
n
:=
B
(
1
n
,
1
n
)
{\displaystyle \pi _{n}\mathrel {:=} \mathrm {B} {\bigl (}{\tfrac {1}{n}},{\tfrac {1}{n}}{\bigr )}}
x
n
+
y
n
=
1
{\displaystyle x^{n}+y^{n}=1}
2
∫
0
1
1
−
x
n
n
d
x
=
1
n
π
n
.
{\textstyle 2\int _{0}^{1}{\sqrt[{n}]{1-x^{n}}}\mathop {\mathrm {d} x} ={\tfrac {1}{n}}\pi _{n}.}
1
4
π
4
=
1
2
ϖ
.
{\displaystyle {\tfrac {1}{4}}\pi _{4}={\tfrac {1}{\sqrt {2}}}\varpi .}
In 1842, Malmsten discovered that[ 47]
∫
0
1
log
(
−
log
x
)
1
+
x
2
d
x
=
π
2
log
π
ϖ
2
.
{\displaystyle \int _{0}^{1}{\frac {\log(-\log x)}{1+x^{2}}}\,dx={\frac {\pi }{2}}\log {\frac {\pi }{\varpi {\sqrt {2}}}}.}
Furthermore,
∫
0
∞
tanh
x
x
e
−
x
d
x
=
log
ϖ
2
π
{\displaystyle \int _{0}^{\infty }{\frac {\tanh x}{x}}e^{-x}\,dx=\log {\frac {\varpi ^{2}}{\pi }}}
and[ 48]
∫
0
∞
e
−
x
4
d
x
=
2
ϖ
2
π
4
,
analogous to
∫
0
∞
e
−
x
2
d
x
=
π
2
,
{\displaystyle \int _{0}^{\infty }e^{-x^{4}}\,dx={\frac {\sqrt {2\varpi {\sqrt {2\pi }}}}{4}},\quad {\text{analogous to}}\,\int _{0}^{\infty }e^{-x^{2}}\,dx={\frac {\sqrt {\pi }}{2}},}
Gaussian integral .
The lemniscate constant appears in the evaluation of the integrals
π
ϖ
=
∫
0
π
2
sin
(
x
)
d
x
=
∫
0
π
2
cos
(
x
)
d
x
{\displaystyle {\frac {\pi }{\varpi }}=\int _{0}^{\frac {\pi }{2}}{\sqrt {\sin(x)}}\,dx=\int _{0}^{\frac {\pi }{2}}{\sqrt {\cos(x)}}\,dx}
ϖ
π
=
∫
0
∞
d
x
cosh
(
π
x
)
{\displaystyle {\frac {\varpi }{\pi }}=\int _{0}^{\infty }{\frac {dx}{\sqrt {\cosh(\pi x)}}}}
John Todd's lemniscate constants are defined by integrals:[ 9]
A
=
∫
0
1
d
x
1
−
x
4
{\displaystyle A=\int _{0}^{1}{\frac {dx}{\sqrt {1-x^{4}}}}}
B
=
∫
0
1
x
2
d
x
1
−
x
4
{\displaystyle B=\int _{0}^{1}{\frac {x^{2}\,dx}{\sqrt {1-x^{4}}}}}
Circumference of an ellipse [ edit ] The lemniscate constant satisfies the equation
π
ϖ
=
2
∫
0
1
x
2
d
x
1
−
x
4
{\displaystyle {\frac {\pi }{\varpi }}=2\int _{0}^{1}{\frac {x^{2}\,dx}{\sqrt {1-x^{4}}}}}
Euler discovered in 1738 that for the rectangular elastica (first and second lemniscate constants)[ 50]
arc
length
⋅
height
=
A
⋅
B
=
∫
0
1
d
x
1
−
x
4
⋅
∫
0
1
x
2
d
x
1
−
x
4
=
ϖ
2
⋅
π
2
ϖ
=
π
4
{\displaystyle {\textrm {arc}}\ {\textrm {length}}\cdot {\textrm {height}}=A\cdot B=\int _{0}^{1}{\frac {\mathrm {d} x}{\sqrt {1-x^{4}}}}\cdot \int _{0}^{1}{\frac {x^{2}\mathop {\mathrm {d} x} }{\sqrt {1-x^{4}}}}={\frac {\varpi }{2}}\cdot {\frac {\pi }{2\varpi }}={\frac {\pi }{4}}}
Now considering the circumference
C
{\displaystyle C}
2
{\displaystyle {\sqrt {2}}}
1
{\displaystyle 1}
2
x
2
+
4
y
2
=
1
{\displaystyle 2x^{2}+4y^{2}=1}
C
2
=
∫
0
1
d
x
1
−
x
4
+
∫
0
1
x
2
d
x
1
−
x
4
{\displaystyle {\frac {C}{2}}=\int _{0}^{1}{\frac {dx}{\sqrt {1-x^{4}}}}+\int _{0}^{1}{\frac {x^{2}\,dx}{\sqrt {1-x^{4}}}}}
Hence the full circumference is
C
=
π
ϖ
+
ϖ
=
3.820197789
…
{\displaystyle C={\frac {\pi }{\varpi }}+\varpi =3.820197789\ldots }
This is also the arc length of the sine curve on half a period:[ 52]
C
=
∫
0
π
1
+
cos
2
(
x
)
d
x
{\displaystyle C=\int _{0}^{\pi }{\sqrt {1+\cos ^{2}(x)}}\,dx}
Analogously to
2
π
=
lim
n
→
∞
|
(
2
n
)
!
B
2
n
|
1
2
n
{\displaystyle 2\pi =\lim _{n\to \infty }\left|{\frac {(2n)!}{\mathrm {B} _{2n}}}\right|^{\frac {1}{2n}}}
B
n
{\displaystyle \mathrm {B} _{n}}
Bernoulli numbers , we have
2
ϖ
=
lim
n
→
∞
(
(
4
n
)
!
H
4
n
)
1
4
n
{\displaystyle 2\varpi =\lim _{n\to \infty }\left({\frac {(4n)!}{\mathrm {H} _{4n}}}\right)^{\frac {1}{4n}}}
H
n
{\displaystyle \mathrm {H} _{n}}
Hurwitz numbers .
^ See:
^ See:
Finch 2003 , p. 420Kobayashi, Hiroyuki; Takeuchi, Shingo (2019), "Applications of generalized trigonometric functions with two parameters", Communications on Pure & Applied Analysis , 18 (3): 1509–1521, arXiv :1903.07407 doi :10.3934/cpaa.2019072 , S2CID 102487670 Asai, Tetsuya (2007), Elliptic Gauss Sums and Hecke L-values at s=1 , arXiv :0707.3711 "A062539 - Oeis" . ^ "A064853 - Oeis" .^ "Lemniscate Constant" .^ "Records set by y-cruncher" . numberworld.org . Retrieved 2024-08-20 .^ "A014549 - Oeis" .^ Neither of these proofs was rigorous from the modern point of view. See Cox 1984 , p. 281
^ a b c Todd, John (January 1975). "The lemniscate constants" . Communications of the ACM 18 (1): 14–19. doi :10.1145/360569.360580 S2CID 85873 . ^ a b "A085565 - Oeis" ."A076390 - Oeis" .^ Carlson, B. C. (2010), "Elliptic Integrals" , in Olver, Frank W. J. ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions ISBN 978-0-521-19225-5 MR 2723248 ^ In particular, Siegel proved that if
G
4
(
ω
1
,
ω
2
)
{\displaystyle \operatorname {G} _{4}(\omega _{1},\omega _{2})}
G
6
(
ω
1
,
ω
2
)
{\displaystyle \operatorname {G} _{6}(\omega _{1},\omega _{2})}
Im
(
ω
2
/
ω
1
)
>
0
{\displaystyle \operatorname {Im} (\omega _{2}/\omega _{1})>0}
ω
1
{\displaystyle \omega _{1}}
ω
2
{\displaystyle \omega _{2}}
G
4
{\displaystyle \operatorname {G} _{4}}
G
6
{\displaystyle \operatorname {G} _{6}}
Eisenstein series . The fact that
ϖ
{\displaystyle \varpi }
G
4
(
ϖ
,
ϖ
i
)
=
1
/
15
{\displaystyle \operatorname {G} _{4}(\varpi ,\varpi i)=1/15}
G
6
(
ϖ
,
ϖ
i
)
=
0.
{\displaystyle \operatorname {G} _{6}(\varpi ,\varpi i)=0.}
Apostol, T. M. (1990). Modular Functions and Dirichlet Series in Number Theory (Second ed.). Springer. p. 12. ISBN 0-387-97127-0
Siegel, C. L. (1932). "Über die Perioden elliptischer Funktionen" . Journal für die reine und angewandte Mathematik 167 : 62–69.
^ In particular, Schneider proved that the beta function
B
(
a
,
b
)
{\displaystyle \mathrm {B} (a,b)}
a
,
b
∈
Q
∖
Z
{\displaystyle a,b\in \mathbb {Q} \setminus \mathbb {Z} }
a
+
b
∉
Z
0
−
{\displaystyle a+b\notin \mathbb {Z} _{0}^{-}}
ϖ
{\displaystyle \varpi }
ϖ
=
1
2
B
(
1
4
,
1
2
)
{\displaystyle \varpi ={\tfrac {1}{2}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )}}
B and G from
B
(
1
2
,
3
4
)
.
{\displaystyle \mathrm {B} {\bigl (}{\tfrac {1}{2}},{\tfrac {3}{4}}{\bigr )}.}
Schneider, Theodor (1941). "Zur Theorie der Abelschen Funktionen und Integrale" . Journal für die reine und angewandte Mathematik . 183 (19): 110–128. doi :10.1515/crll.1941.183.110 . S2CID 118624331 .
^ G. V. Choodnovsky: Algebraic independence of constants connected with the functions of analysis , Notices of the AMS 22, 1975, p. A-486
^ G. V. Chudnovsky: Contributions to The Theory of Transcendental Numbers , American Mathematical Society, 1984, p. 6
^ In fact,
π
=
2
2
M
3
(
1
,
1
2
)
M
′
(
1
,
1
2
)
=
1
G
3
M
′
(
1
,
1
2
)
.
{\displaystyle \pi =2{\sqrt {2}}{\frac {M^{3}\left(1,{\frac {1}{\sqrt {2}}}\right)}{M'\left(1,{\frac {1}{\sqrt {2}}}\right)}}={\frac {1}{G^{3}M'\left(1,{\frac {1}{\sqrt {2}}}\right)}}.}
Borwein, Jonathan M.; Borwein, Peter B. (1987). Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity (First ed.). Wiley-Interscience. ISBN 0-471-83138-7
^ Nesterenko, Y. V.; Philippon, P. (2001). Introduction to Algebraic Independence Theory . Springer. p. 27. ISBN 3-540-41496-7 ^ See:
^ "A113847 - Oeis" .^ Cremona, J. E. (1997). Algorithms for Modular Elliptic Curves Cambridge University Press . ISBN 0521598206 ^ In fact, the series
∑
n
=
1
∞
ν
(
n
)
n
s
{\textstyle \sum _{n=1}^{\infty }{\frac {\nu (n)}{n^{s}}}}
ℜ
s
>
5
/
6
{\displaystyle \operatorname {\Re } s>5/6}
^ Murty, Vijaya Kumar (1995). Seminar on Fermat's Last Theorem . American Mathematical Society . p. 16. ISBN 9780821803134 ^ Cohen, Henri (1993). A Course in Computational Algebraic Number Theory . Springer-Verlag. pp. 382–406. ISBN 978-3-642-08142-2 ^ "Elliptic curve with LMFDB label 32.a3 (Cremona label 32a2)" . The L-functions and modular forms database .^ The function
F
{\displaystyle F}
2
{\displaystyle 2}
32
{\displaystyle 32}
new form and it satisfies the functional equation
F
(
−
1
τ
)
=
−
τ
2
32
F
(
τ
1
32
)
.
{\displaystyle F\left(-{\frac {1}{\tau }}\right)=-{\frac {\tau ^{2}}{32}}F\left({\frac {\tau {\vphantom {1}}}{32}}\right).}
^ The
ν
{\displaystyle \nu }
ξ
{\displaystyle \xi }
ξ
(
p
n
)
=
{
N
p
′
,
p
∈
P
,
n
=
1
ξ
(
p
n
−
1
)
+
χ
(
p
)
n
,
p
∈
P
,
n
≥
2
{\displaystyle \xi (p^{n})={\begin{cases}{\mathcal {N}}_{p}',&p\in \mathbb {P} ,\,n=1\\[5mu]\xi (p^{n-1})+\chi (p)^{n},&p\in \mathbb {P} ,\,n\geq 2\end{cases}}}
N
p
′
{\displaystyle {\mathcal {N}}_{p}'}
a
2
+
b
2
=
p
,
p
∈
P
{\displaystyle a^{2}+b^{2}=p,\quad p\in \mathbb {P} }
a
,
b
{\displaystyle a,b}
Fermat's theorem on sums of two squares ) and
χ
{\displaystyle \chi }
Dirichlet character from the Leibniz formula for π; also
∑
d
|
n
χ
(
d
)
=
ξ
(
n
)
{\displaystyle \sum _{d|n}\chi (d)=\xi (n)}
n
{\displaystyle n}
ν
{\displaystyle \nu }
ξ
{\displaystyle \xi }
∑
k
=
0
n
(
−
1
)
k
ξ
(
4
k
+
1
)
ξ
(
4
n
−
4
k
+
1
)
=
ν
(
2
n
+
1
)
{\displaystyle \sum _{k=0}^{n}(-1)^{k}\xi (4k+1)\xi (4n-4k+1)=\nu (2n+1)}
n
{\displaystyle n}
^ The
ν
{\displaystyle \nu }
∑
z
∈
G
;
z
z
¯
=
n
z
=
ν
(
n
)
{\displaystyle \sum _{z\in \mathbb {G} ;\,z{\overline {z}}=n}z=\nu (n)}
n
{\displaystyle n}
G
{\displaystyle \operatorname {\mathbb {G} } }
Gaussian integers of the form
(
−
1
)
a
±
b
−
1
2
(
a
±
b
i
)
{\displaystyle (-1)^{\frac {a\pm b-1}{2}}(a\pm bi)}
a
{\displaystyle a}
b
{\displaystyle b}
ξ
{\displaystyle \xi }
|
{
z
:
z
∈
G
∧
z
z
¯
=
n
}
|
=
ξ
(
n
)
{\displaystyle \left|\{z:z\in \mathbb {G} \land z{\overline {z}}=n\}\right|=\xi (n)}
n
{\displaystyle n}
^ Rubin, Karl (1987). "Tate-Shafarevich groups and L-functions of elliptic curves with complex multiplication" . Inventiones Mathematicae . 89 : 528. ^ "Newform orbit 1.12.a.a" . The L-functions and modular forms database .^ Levin (2006)
^ Hyde (2014) proves the validity of a more general Wallis-like formula for clover curves; here the special case of the lemniscate is slightly transformed, for clarity.
^ Hyde, Trevor (2014). "A Wallis product on clovers" (PDF) . The American Mathematical Monthly . 121 (3): 237–243. doi :10.4169/amer.math.monthly.121.03.237 . S2CID 34819500 . ^ Bottazzini, Umberto ; Gray, Jeremy (2013). Hidden Harmony – Geometric Fantasies: The Rise of Complex Function Theory . Springer. doi :10.1007/978-1-4614-5725-1 . ISBN 978-1-4614-5724-4 ^ Todd (1975)
^ Cox 1984 , p. 307, eq. 2.21 for the first equality. The second equality can be proved by using the pentagonal number theorem .^ Berndt, Bruce C. (1998). Ramanujan's Notebooks Part V . Springer. ISBN 978-1-4612-7221-2 ^ This formula can be proved by hypergeometric inversion : Let
a
(
q
)
=
∑
m
,
n
∈
Z
q
m
2
+
m
n
+
n
2
{\displaystyle \operatorname {a} (q)=\sum _{m,n\in \mathbb {Z} }q^{m^{2}+mn+n^{2}}}
q
∈
C
{\displaystyle q\in \mathbb {C} }
|
q
|
<
1
{\displaystyle \left|q\right|<1}
a
(
q
)
=
2
F
1
(
1
3
,
2
3
,
1
,
z
)
{\displaystyle \operatorname {a} (q)={}_{2}F_{1}\left({\frac {1}{3}},{\frac {2}{3}},1,z\right)}
q
=
exp
(
−
2
π
3
2
F
1
(
1
/
3
,
2
/
3
,
1
,
1
−
z
)
2
F
1
(
1
/
3
,
2
/
3
,
1
,
z
)
)
{\displaystyle q=\exp \left(-{\frac {2\pi }{\sqrt {3}}}{\frac {{}_{2}F_{1}(1/3,2/3,1,1-z)}{{}_{2}F_{1}(1/3,2/3,1,z)}}\right)}
z
∈
C
∖
{
0
,
1
}
{\displaystyle z\in \mathbb {C} \setminus \{0,1\}}
z
=
1
4
(
3
3
−
5
)
{\textstyle z={\tfrac {1}{4}}{\bigl (}3{\sqrt {3}}-5{\bigr )}}
^ Eymard, Pierre; Lafon, Jean-Pierre (2004). The Number Pi . American Mathematical Society. ISBN 0-8218-3246-8 ^ Garrett, Paul. "Level-one elliptic modular forms" (PDF) . University of Minnesota . ^ The formula follows from the hypergeometric transformation
3
F
2
(
1
4
,
1
2
,
3
4
,
1
,
1
,
16
z
(
1
−
z
)
2
(
1
+
z
)
4
)
=
(
1
+
z
)
2
F
1
(
1
2
,
1
2
,
1
,
z
)
2
{\displaystyle {}_{3}F_{2}\left({\frac {1}{4}},{\frac {1}{2}},{\frac {3}{4}},1,1,16z{\frac {(1-z)^{2}}{(1+z)^{4}}}\right)=(1+z)\,{}_{2}F_{1}\left({\frac {1}{2}},{\frac {1}{2}},1,z\right)^{2}}
z
=
λ
(
1
+
5
i
)
{\displaystyle z=\lambda (1+5i)}
λ
{\displaystyle \lambda }
modular lambda function .
^ Khrushchev, Sergey (2008). Orthogonal Polynomials and Continued Fractions (First ed.). Cambridge University Press. ISBN 978-0-521-85419-1
4
[
Γ
(
3
+
s
/
4
)
/
Γ
(
1
+
s
/
4
)
]
2
{\displaystyle 4[\Gamma (3+s/4)/\Gamma (1+s/4)]^{2}}
4
[
Γ
(
(
3
+
s
)
/
4
)
/
Γ
(
(
1
+
s
)
/
4
)
]
2
{\displaystyle 4[\Gamma ((3+s)/4)/\Gamma ((1+s)/4)]^{2}}
^ Khrushchev, Sergey (2008). Orthogonal Polynomials and Continued Fractions (First ed.). Cambridge University Press. ISBN 978-0-521-85419-1 ^ Perron, Oskar (1957). Die Lehre von den Kettenbrüchen: Band II (in German) (Third ed.). B. G. Teubner.^ "A062540 - OEIS" . oeis.org . Retrieved 2022-09-14 .^ "A053002 - OEIS" . oeis.org .^ Blagouchine, Iaroslav V. (2014). "Rediscovery of Malmsten's integrals, their evaluation by contour integration methods and some related results" . The Ramanujan Journal . 35 (1): 21–110. doi :10.1007/s11139-013-9528-5 . S2CID 120943474 . ^ "A068467 - Oeis" .^ Levien (2008)
^ Adlaj, Semjon (2012). "An Eloquent Formula for the Perimeter of an Ellipse" (PDF) . American Mathematical Society . p. 1097. One might also observe that the length of the "sine" curve over half a period, that is, the length of the graph of the function sin(t) from the point where t = 0 to the point where t = π , is
2
l
(
1
/
2
)
=
L
+
M
{\displaystyle {\sqrt {2}}l(1/{\sqrt {2}})=L+M}
M
=
1
/
G
=
π
/
ϖ
{\displaystyle M=1/G=\pi /\varpi }
L
=
π
/
M
=
G
π
=
ϖ
{\displaystyle L=\pi /M=G\pi =\varpi }













![{\displaystyle {\begin{aligned}\varpi &=2\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}={\sqrt {2}}\int _{0}^{\infty }{\frac {\mathrm {d} t}{\sqrt {1+t^{4}}}}=\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {t-t^{3}}}}=\int _{1}^{\infty }{\frac {\mathrm {d} t}{\sqrt {t^{3}-t}}}\\[6mu]&=4\int _{0}^{\infty }{\Bigl (}{\sqrt[{4}]{1+t^{4}}}-t{\Bigr )}\,\mathrm {d} t=2{\sqrt {2}}\int _{0}^{1}{\sqrt[{4}]{1-t^{4}}}\mathop {\mathrm {d} t} =3\int _{0}^{1}{\sqrt {1-t^{4}}}\,\mathrm {d} t\\[2mu]&=2K(i)={\tfrac {1}{2}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )}={\tfrac {1}{2{\sqrt {2}}}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{4}}{\bigr )}={\frac {\Gamma (1/4)^{2}}{2{\sqrt {2\pi }}}}={\frac {2-{\sqrt {2}}}{4}}{\frac {\zeta (3/4)^{2}}{\zeta (1/4)^{2}}}\\[5mu]&=2.62205\;75542\;92119\;81046\;48395\;89891\;11941\ldots ,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa00a5743dc4d1915700def2e48ae2b95514bf6f)




![{\displaystyle {\begin{aligned}A&={\frac {\varpi }{2}}={\tfrac {1}{4}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )},\\[3mu]B&={\frac {\pi }{2\varpi }}={\tfrac {1}{4}}\mathrm {B} {\bigl (}{\tfrac {1}{2}},{\tfrac {3}{4}}{\bigr )}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1b5bf31d2eec5d57cb4a4af2721754d24962c5e)









![{\displaystyle \nu (p^{n})={\begin{cases}p-{\mathcal {N}}_{p},&p\in \mathbb {P} ,\,n=1\\[5mu]0,&p=2,\,n\geq 2\\[5mu]\nu (p)\nu (p^{n-1})-p\nu (p^{n-2}),&p\in \mathbb {P} \setminus \{2\},\,n\geq 2\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f28f42f8065c750aef0016cb73c652a0daeb342a)

































![{\displaystyle \sum _{z\in \mathbb {Z} [i]\setminus \{0\}}{\frac {1}{z^{4}}}=G_{4}(i)={\frac {\varpi ^{4}}{15}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2c020975bd00f51d682f805befa01df23988448)
![{\displaystyle \mathbb {Z} [i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)







![{\displaystyle \varpi =\pi {\sqrt[{4}]{32}}e^{-{\frac {\pi }{3}}}{\biggl (}\sum _{n=-\infty }^{\infty }(-1)^{n}e^{-2n\pi (3n+1)}{\biggr )}^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e92daf3dbe5e4b505b6c7a497da581035294fb33)













![{\displaystyle {\begin{aligned}\varpi &=[2,1,1,1,1,1,4,1,2,\ldots ],\\[8mu]2\varpi &=[5,4,10,2,1,2,3,29,\ldots ],\\[5mu]{\frac {\varpi }{2}}&=[1,3,4,1,1,1,5,2,\ldots ],\\[2mu]{\frac {\varpi }{\pi }}&=[0,1,5,21,3,4,14,\ldots ].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77b83715e21dc69253b7047b2045b6e482802fdd)





![{\textstyle 2\int _{0}^{1}{\sqrt[{n}]{1-x^{n}}}\mathop {\mathrm {d} x} ={\tfrac {1}{n}}\pi _{n}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba1088ee33b310fd26307c26b917b43a7a9211ae)









































![{\displaystyle \xi (p^{n})={\begin{cases}{\mathcal {N}}_{p}',&p\in \mathbb {P} ,\,n=1\\[5mu]\xi (p^{n-1})+\chi (p)^{n},&p\in \mathbb {P} ,\,n\geq 2\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d3c39f2c333fe2d73f8faad95d5d0625cd84965)





















![{\displaystyle 4[\Gamma (3+s/4)/\Gamma (1+s/4)]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7dbbf0163687acf39aec82572e89e1cfc9814f41)
![{\displaystyle 4[\Gamma ((3+s)/4)/\Gamma ((1+s)/4)]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e3daa83f9526cd20ebe1bddfefa93546ba20d1d)



