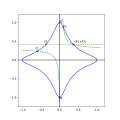
.
import matplotlib.pyplot as plt
import numpy as np
import math
from collections import namedtuple
# Utility type
Point = namedtuple('Point', ['x', 'y'])
d = -30
def edwards_y(x):
return np.sqrt((x*x - 1)/(d*x*x - 1))
# Draw Edwards curve
x = np.linspace(-1,1,200)
ypos = edwards_y(x)
yneg = -ypos
plt.figure(figsize=[6, 6])
plt.plot(x,ypos, 'b')
plt.plot(x,yneg, 'b')
# Draw neutral point
plt.scatter(0,1)
plt.annotate("O", (0.01, 1.01))
# Draw order 2 point
plt.scatter(0,-1)
plt.annotate("O'", (0.01, -1.05))
# Draw the points P1 and P2
P1=Point(-0.6, edwards_y(-0.6))
P2=Point(0.1, edwards_y(0.1))
plt.scatter(*P1)
plt.annotate("P1", (P1.x-0.05, P1.y+0.05))
plt.scatter(*P2)
plt.annotate("P2", P2)
# Compute and draw P1 + P2
def edwards_sum(x1,y1,x2,y2):
return ( (x1*y2+x2*y1)/(1+d*x1*x2*y1*y2) , (y1*y2 - x1*x2)/(1-d*x1*x2*y1*y2) )
P3 = Point(*edwards_sum(*P1, *P2))
plt.scatter(*P3)
plt.annotate("P3", (P3.x-0.05, P3.y+0.05))
P3_ = Point(-P3.x, P3.y)
plt.scatter(*P3_)
plt.annotate("-(P1+P2)", (P3_.x+0.01, P3_.y+0.05))
# Draw the line that connects P3 and -P3
plt.axhline(P3.y, linestyle='--', color="grey")
# Draw the conic that P1, P2 and -(P1+P2) belong to
def conic_coefs(x1,y1,x2,y2):
"Computes coeffitiens of the quadratic form Axy + Bx + Cx + D"
return (x1-x2 + (x1*y2-x2*y1),
(x2*y2-x1*y1)+y1*y2*(x2-x1),
x1*x2*(y1-y2),
x1*x2*(y1-y2)
)
def conic_y(x, A,B,C,D):
return -(B*x + D)/(A*x + C)
A,B,C,D = conic_coefs(*P1,*P2)
# Left and right branches of the hyperbole
xleft = np.linspace(-1,0.003,50)
xright = np.linspace(P2[0] - 0.02, 1.1, 50)
yleft = conic_y(xleft, A,B,C,D)
yright = conic_y(xright, A,B,C,D)
plt.plot(xleft, yleft,"--", color="green")
plt.plot(xright, yright,"--", color="green")
# Draw axis lines
plt.axhline(0, color='black')
plt.axvline(0, color='black')
# Set same scale on x and y
plt.gca().set_aspect('equal', adjustable='box')
plt.savefig("Add_points_Edwards.svg")