File:StationaryStatesAnimation.gif
Appearance
StationaryStatesAnimation.gif (300 × 280 pixels, file size: 223 KB, MIME type: image/gif, looped, 41 frames)
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 18:21, 20 March 2011 | 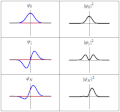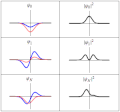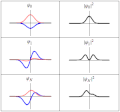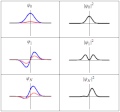 | 300 × 280 (223 KB) | Sbyrnes321 | {{Information |Description ={{en|1=Three wavefunction solutions to the Time-Dependent Schrödinger equation for a harmonic oscillator. Left: The real part (blue) and imaginary part (red) of the wavefunction. Right: The probability of finding the partic |
File usage
The following 6 pages use this file:
Global file usage
The following other wikis use this file:
- Usage on ar.wikipedia.org
- Usage on ast.wikipedia.org
- Usage on az.wikipedia.org
- Usage on bn.wikipedia.org
- Usage on bs.wikipedia.org
- Usage on de.wikipedia.org
- Usage on el.wikipedia.org
- Usage on eo.wikipedia.org
- Usage on es.wikipedia.org
- Usage on fa.wikipedia.org
- Usage on ga.wikipedia.org
- Usage on gl.wikipedia.org
- Usage on he.wikipedia.org
- Usage on hy.wikipedia.org
- Usage on ia.wikipedia.org
- Usage on id.wikipedia.org
- Usage on ja.wikipedia.org
- Usage on lt.wikipedia.org
- Usage on mk.wikipedia.org
- Usage on pa.wikipedia.org
- Usage on pl.wikipedia.org
- Usage on pnb.wikipedia.org
- Usage on ro.wikipedia.org
- Usage on sl.wikipedia.org
- Usage on ta.wikipedia.org
- Usage on tl.wikipedia.org
- Usage on tr.wikipedia.org
- Usage on uk.wikipedia.org
- Usage on uz.wikipedia.org
- Usage on vi.wikipedia.org
- Usage on www.wikidata.org
- Usage on zh.wikipedia.org


