File:Liquid Crystal based Spatial Light Modulator.gif
Page contents not supported in other languages.
Tools
Actions
General
In other projects
Appearance
Liquid_Crystal_based_Spatial_Light_Modulator.gif (360 × 263 pixels, file size: 947 KB, MIME type: image/gif, looped, 80 frames)
| This is a file from the Wikimedia Commons. Information from its description page there is shown below. Commons is a freely licensed media file repository. You can help. |
Summary
| DescriptionLiquid Crystal based Spatial Light Modulator.gif |
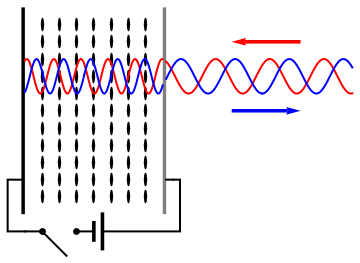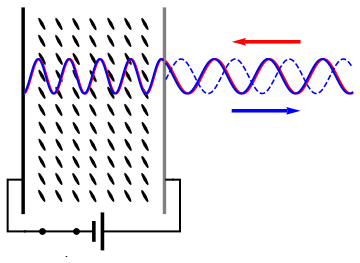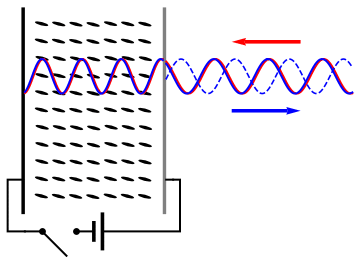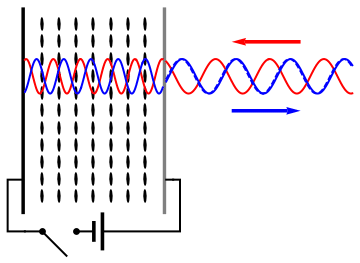
English: As (nematic) liquid crystals are birifrangent and their orientation can be changed applying an electric field, it is possible to change the refractive index seen by an incident wave applying a voltage to a liquid crystal cell and thus control the phase retardation of the reflected wave. |
| Date | |
| Source | https://twitter.com/j_bertolotti/status/1144556106192183296 |
| Author | Jacopo Bertolotti |
| Permission (Reusing this file) |
https://twitter.com/j_bertolotti/status/1030470604418428929 |
Mathematica 11.0 code
k1 = 2;
k2 = 4;
p1 = Table[
Show[
Graphics[{Polygon[{{-4.2, -6}, {-4, -6}, {-4, 6}, {-4.2, 6}}], Gray, Polygon[{{4.2, -6}, {4, -6}, {4, 6}, {4.2, 6}}], Black, Thick, Line[{{-4.1, -4}, {-5, -4}, {-5, -7}, {-3, -7}}], Disk[{-3, -7}, 0.2], Disk[{-1, -7}, 0.2], Line[{{-1, -7}, {0, -7}}], Line[{{0.5, -7}, {5, -7}, {5, -4}, {4.2, -4}}], Line[{{-3, -7}, {-3 + 2/Sqrt[2], -7 - 2/Sqrt[2]}}], Thickness[0.01], Line[{{0, -7.5}, {0, -6.5}}],
Line[{{0.5, -8}, {0.5, -6}}], Table[Rotate[Disk[{x, y}, {0.1, 0.4}], 0], {x, -3, 3, 1}, {y, -5, 5, 1}], Red, Arrow[{{12, 4}, {8, 4}}], Blue, Arrow[{{8, 0}, {12, 0}}] }],
Plot[Sin[k1 x] + 2, {x, 4.2, 15}, Axes -> False, PlotRange -> All, PlotStyle -> {Red, Thick}], Plot[Sin[k2 x + 4 (k1 - k2)] + 2, {x, -4, 4}, Axes -> False, PlotRange -> All, PlotStyle -> {Red, Thick}]
,
Plot[-Sin[32 - 4 k1 + \[Pi] + k2 (4 + x)] + 2, {x, -4, 4}, Axes -> False, PlotRange -> All, PlotStyle -> {Blue, Thick}],
Plot[-Sin[32 - 4 k1 + \[Pi] + 4 k2 + k1 x + 4 (k2 - k1)] + 2, {x, 4.2, 15}, Axes -> False, PlotRange -> All, PlotStyle -> {Blue, Thick}]
]
, {\[Phi], 2 \[Pi], 0, -0.4}];
k1 = 2;
k2 = 4;
k2old = 4;
knew = 2.5;
p2 = Table[
k2 = \[Phi]/(2 \[Pi]) knew + (1 - \[Phi]/(2 \[Pi])) k2old;
Show[
Graphics[{Polygon[{{-4.2, -6}, {-4, -6}, {-4, 6}, {-4.2, 6}}], Gray, Polygon[{{4.2, -6}, {4, -6}, {4, 6}, {4.2, 6}}], Black, Thick, Line[{{-4.1, -4}, {-5, -4}, {-5, -7}, {-3, -7}}], Disk[{-3, -7}, 0.2], Disk[{-1, -7}, 0.2], Line[{{-1, -7}, {0, -7}}], Line[{{0.5, -7}, {5, -7}, {5, -4}, {4.2, -4}}], Line[{{-3, -7}, {-1, -7}}], Thickness[0.01], Line[{{0, -7.5}, {0, -6.5}}], Line[{{0.5, -8}, {0.5, -6}}]
, Table[Rotate[Disk[{x, y}, {0.1, 0.4}], \[Phi]/4], {x, -3, 3, 1}, {y, -5, 5, 1}], Red, Arrow[{{12, 4}, {8, 4}}], Blue, Arrow[{{8, 0}, {12, 0}}] }],
Plot[Sin[k1 x] + 2, {x, 4.2, 15}, Axes -> False, PlotRange -> All, PlotStyle -> {Red, Thick}], Plot[Sin[k2 x + 4 (k1 - k2)] + 2, {x, -4, 4}, Axes -> False, PlotRange -> All, PlotStyle -> {Red, Thick}]
,
Plot[-Sin[32 - 4 k1 + \[Pi] + k2 (4 + x)] + 2, {x, -4, 4}, Axes -> False, PlotRange -> All, PlotStyle -> {Blue, Thick}],
Plot[-Sin[32 - 4 k1 + \[Pi] + 4 k2 + k1 x + 4 (k2 - k1)] + 2, {x, 4.2, 15}, Axes -> False, PlotRange -> All, PlotStyle -> {Blue, Thick}]
,
Plot[-Sin[32 - 4 k1 + \[Pi] + 4 k2old + k1 x + 4 (k2old - k1)] + 2, {x, 4.2, 15}, Axes -> False, PlotRange -> All, PlotStyle -> {Blue, Dashed}]
]
, {\[Phi], 0, 2 \[Pi], 0.2}];
k1 = 2;
k2 = 4;
k2old = 4;
knew = 2.5;
p3 = Table[
k2 = \[Phi]/(2 \[Pi]) knew + (1 - \[Phi]/(2 \[Pi])) k2old;
Show[
Graphics[{Polygon[{{-4.2, -6}, {-4, -6}, {-4, 6}, {-4.2, 6}}], Gray, Polygon[{{4.2, -6}, {4, -6}, {4, 6}, {4.2, 6}}], Black, Thick, Line[{{-4.1, -4}, {-5, -4}, {-5, -7}, {-3, -7}}], Disk[{-3, -7}, 0.2], Disk[{-1, -7}, 0.2], Line[{{-1, -7}, {0, -7}}], Line[{{0.5, -7}, {5, -7}, {5, -4}, {4.2, -4}}], Line[{{-3, -7}, {-3 + 2/Sqrt[2], -7 - 2/Sqrt[2]}}], Thickness[0.01], Line[{{0, -7.5}, {0, -6.5}}],
Line[{{0.5, -8}, {0.5, -6}}], Table[Rotate[Disk[{x, y}, {0.1, 0.4}], \[Phi]/4], {x, -3, 3, 1}, {y, -5, 5, 1}], Red, Arrow[{{12, 4}, {8, 4}}], Blue, Arrow[{{8, 0}, {12, 0}}] }],
Plot[Sin[k1 x] + 2, {x, 4.2, 15}, Axes -> False, PlotRange -> All, PlotStyle -> {Red, Thick}], Plot[Sin[k2 x + 4 (k1 - k2)] + 2, {x, -4, 4}, Axes -> False, PlotRange -> All, PlotStyle -> {Red, Thick}]
,
Plot[-Sin[32 - 4 k1 + \[Pi] + k2 (4 + x)] + 2, {x, -4, 4}, Axes -> False, PlotRange -> All, PlotStyle -> {Blue, Thick}]
,
Plot[-Sin[32 - 4 k1 + \[Pi] + 4 k2 + k1 x + 4 (k2 - k1)] + 2, {x, 4.2, 15}, Axes -> False, PlotRange -> All, PlotStyle -> {Blue, Thick}]
,
Plot[-Sin[32 - 4 k1 + \[Pi] + 4 k2old + k1 x + 4 (k2old - k1)] + 2, {x, 4.2, 15}, Axes -> False, PlotRange -> All, PlotStyle -> {Blue, Dashed}]
]
, {\[Phi], 2 \[Pi], 0, -0.2}];
ListAnimate[Join[p1, p2, p3]]
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
| This file is made available under the Creative Commons CC0 1.0 Universal Public Domain Dedication. | |
| The person who associated a work with this deed has dedicated the work to the public domain by waiving all of their rights to the work worldwide under copyright law, including all related and neighboring rights, to the extent allowed by law. You can copy, modify, distribute and perform the work, even for commercial purposes, all without asking permission.
http://creativecommons.org/publicdomain/zero/1.0/deed.enCC0Creative Commons Zero, Public Domain Dedicationfalsefalse |
Captions
Schematic working of a LCOS SLM
Items portrayed in this file
depicts
some value
28 June 2019
image/gif
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 13:00, 28 June 2019 |  | 360 × 263 (947 KB) | Berto | User created page with UploadWizard |
File usage
The following page uses this file:
Global file usage
The following other wikis use this file:
- Usage on ar.wikipedia.org
Metadata
This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.
If the file has been modified from its original state, some details may not fully reflect the modified file.
| GIF file comment | Created with the Wolfram Language : www.wolfram.com |
|---|