File:Golden number and Platonic dodecahedron exhibited through golden tilings.svg

Original file (SVG file, nominally 1,131 × 699 pixels, file size: 19 KB)
| This is a file from the Wikimedia Commons. Information from its description page there is shown below. Commons is a freely licensed media file repository. You can help. |
Summary
| DescriptionGolden number and Platonic dodecahedron exhibited through golden tilings.svg |
English:
When a face of this Platonic dodecahedron is entirely tiled, like the regular pentagon on this image, the face contains
Every element of any type is called golden triangle, because of its length ratio of two edges:
Any similar elements of tilings are congruent. All tilings are contructed edge‑to‑edge: any boundary between two adjacent elements is a full edge of one and the other element, even if this common edge is on an edge of the dodecahedron, when the two adjacent elements are not coplanar. A first projection of this Platonic dodecahedron distorts neither the face of solid at the center of the drawing nor all concentric regular decagons that it bears. One of them is a star decagon with interlaces edges. This first projection gives the solid a regular outline: a regular decagon again, but not oriented like the previous convex decagons. The ten edges of the outline are ten images of edges of the solid reduced to the same scale by the projection. On the right, a small drawing of the same solid represents its hidden edges in dashed lines. We assume it is the same dodecahedron since we recognize certain parts of tilings that remain, notably at the center of the drawing where a regular pyramid has three faces tiled each by two golden triangles. This second projection does not distort the base of this pyramid, nor the red hexagonal cross section which is regular. Its six edges are parallel to those of the outline not shrinked by the projection, by disregarding the reduction of the whole projection relative to the first one. On the left at the image bottom, two curved arrows represent two direct similarities. Their composition enlarges a smallest element of tilings. Their two successive ratios are written near the arrows. Why a Français : Quand une face de ce dodécaèdre de Platon est entièrement pavée, comme le pentagone régulier dans cette image, elle contient
Tout élément quel que soit sa forme s’appelle un triangle d’or, en raison d’un rapport des longueurs de deux côtés :
N’importe quels éléments de pavage qui sont semblables peuvent se superposer exactement, disons plus savamment qu’ils sont isométriques. Ces pavages sont construits bord à bord : toute frontière entre deux éléments adjacents est un côté entier de l’un et l’autre élément, même si ce côté commun est sur une arête du dodécaèdre, quand les deux éléments adjacents ne sont pas coplanaires. Une première projection du dodécaèdre de Platon ne déforme ni la face du solide au centre du dessin, ni tous les décagones réguliers concentriques qu’elle porte. L’un d’eux est un décagone étoilé aux côtés entrelacés. Cette première projection donne au solide un contour régulier : encore un décagone régulier, mais qui n’est pas orienté comme les décagones convexes précédents. Les dix côtés du contour sont dix images d’arêtes rétrécies à la même échelle par la projection. À droite, un petit dessin du même solide représente ses arêtes cachées en pointillés. Nous supposons qu’il s’agit du même dodécaèdre puisque nous reconnaissons certaines parties du pavage qui subsistent, notamment au centre du dessin où une pyramide régulière a trois faces pavées chacune de deux triangles d’or. Cette seconde projection ne déforme pas la base de cette pyramide, ni la section hexagonale rouge qui est régulière. Ses six côtés sont parallèles aux arêtes du contour non rétrécies par la projection, en faisant abstraction de la réduction de l’ensemble de la projection par rapport à la première. |
| Date | |
| Source | Own work |
| Author | Arthur Baelde |
| SVG development InfoField | This /Baelde was created with a text editor. |
Licensing
- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.
Captions
Items portrayed in this file
depicts
some value
3 September 2021
image/svg+xml
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 13:14, 7 September 2021 |  | 1,131 × 699 (19 KB) | Arthur Baelde | some more lines colored and thick, corresponding to certain lengths |
| 12:43, 3 September 2021 | 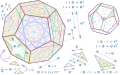 | 1,131 × 699 (19 KB) | Arthur Baelde | Uploaded own work with UploadWizard |
File usage
The following page uses this file:
Global file usage
The following other wikis use this file:
- Usage on fr.wikipedia.org
Metadata
This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.
If the file has been modified from its original state, some details may not fully reflect the modified file.
| Width | 1131 |
|---|---|
| Height | 699 |










