File:GCD through successive subtractions.svg

Original file (SVG file, nominally 660 × 825 pixels, file size: 5 KB)
| This is a file from the Wikimedia Commons. Information from its description page there is shown below. Commons is a freely licensed media file repository. You can help. |
Summary
| DescriptionGCD through successive subtractions.svg |
English: The set of common divisors of two given natural numbers is the set of divisors of one and only one natural number, called the “greatest common divisor” of the initial pair. To prove its existence, it is sufficient to exhibit we can always calculate it, from any pair of natural numbers. How to understand “greatest”? The order in question is divisibility: a partial order on set ℕ of natural numbers. For example, 2 is a common divisor
 that can be written: that can be written:  We will soon calculate the greatest common divisor We will soon calculate the greatest common divisor   Zero is multiple of any natural number, in other words, zero is the greatest element of ℕ for divisibility. Zero is multiple of any natural number, in other words, zero is the greatest element of ℕ for divisibility.  is not the greatest natural number for the usual order relation, of which the symbol is not the greatest natural number for the usual order relation, of which the symbol  The least element of ℕ for divisibility is 1. The least element of ℕ for divisibility is 1.
Under the algorithm of the image, Instead of replacing A novice in coding can copy and paste in a window dedicated to JavaScript one of the following comparisons, and then command the execution: /* To open a Firefox window
dedicated to JavaScript code: Shift + F4 */
d = r = k = 182; p = 238; // example of input values,
// that we can replace with two other natural numbers
if( s = p){ // if the common value of s and p is not zero
while(r){ // while the value of r is not zero
if(r < s){ // in this case, reverse the values of r and s
d = s; s = r; r = d }
r = r-s } // end of the loop 'while(r)'
d = s } // end of the block that begins with 'if( s = p)'
" GCD("+ k +", "+ p +") = "+ d; // output: a String object
// Keyboard shortcut in Firefox to execute the code: Ctrl + L
On the image top, try{ // in case of error in this block,
// execution failure of this code block, go to 'catch'
d = r = k = 408; p = 255; // example of input values
var b; // global scope declaration
s = function(n){
// to test the value of parameter n: is it a natural number?
b = n.constructor == Number; // Boolean value
if( !b // first incorrect case
|| n < 0 || n != Math.floor(n) // other incorrect cases
) throw n
// in one of the previous cases, n is thrown as error
}; // end of assignment to variable s
s(k); s(p); // verifications
if( s = p){ // if the common value of s and p is not zero
while(r){
if(r < s){d = s; s = r; r = d} r = r-s } d = s }
" GCD("+ k +", "+ p +") = "+ d
}catch(e){ // in case of error (if e is thrown)
" "+( b ? e +" is not a natural number.":
" Incorrect code.")
}
   is the irreducible form is the irreducible form  Two natural numbers of which the GCD is 1 are called coprime integers. Two natural numbers of which the GCD is 1 are called coprime integers.Français : Voir la version en français… |
| Date | |
| Source | Own work |
| Author | Arthur Baelde |
| Other versions | |
| SVG development InfoField | This /Baelde was created with a text editor. |
Licensing
- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.
Captions
Items portrayed in this file
depicts
some value
27 June 2018
5,165 byte
825 pixel
660 pixel
image/svg+xml
c583b794c4f66ad732df5117f364c8bb8e54de72
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 13:12, 26 April 2024 | 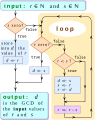 | 660 × 825 (5 KB) | Arthur Baelde | more legible |
| 09:06, 27 June 2018 |  | 660 × 825 (5 KB) | Arthur Baelde | User created page with UploadWizard |
File usage
The following 2 pages use this file:
Global file usage
The following other wikis use this file:
- Usage on bo.wikipedia.org
- Usage on jv.wikipedia.org
Metadata
This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.
If the file has been modified from its original state, some details may not fully reflect the modified file.
| Width | 660 |
|---|---|
| Height | 825 |





























