File:Ensemble quantum 1DOF canonical.png
Page contents not supported in other languages.
Tools
Actions
General
In other projects
Appearance

Size of this preview: 600 × 600 pixels. Other resolutions: 240 × 240 pixels | 480 × 480 pixels | 900 × 900 pixels.
Original file (900 × 900 pixels, file size: 78 KB, MIME type: image/png)
| This is a file from the Wikimedia Commons. Information from its description page there is shown below. Commons is a freely licensed media file repository. You can help. |
Summary
| DescriptionEnsemble quantum 1DOF canonical.png |
English: Ensemble canonically distributed over energy, for a quantum system consisting of one particle in a potential well. |
| Date | |
| Source | Own work |
| Author | Nanite |
Source
This plot was created with Matplotlib.
Python source code. Requires matplotlib.
from pylab import *
figformat = '.png'
saveopts = {'dpi':300} #, 'bbox_inches':'tight', 'transparent':True, 'frameon':True}
seterr(divide='ignore')
# Very important number, smaller means more classical (finer-spaced discrete levels, larger means more quantum (fewer discrete levels)
hbar = 0.7/(2*pi)
temp_canonical = 4.1
energy_microcanonical = -2.0
range_microcanonical = 1.0
micro_e0 = energy_microcanonical - 0.5*range_microcanonical
micro_e1 = energy_microcanonical + 0.5*range_microcanonical
def potential(x):
return x**6 + 4*x**3 - 5*x**2 - 4*x
x = linspace(-2.5,2.5,1001)
dx = x[1] - x[0]
U = potential(x)
mass = 1.0
# compute pixel edges, used for pcolormesh.
xcorners = zeros(len(x)+1)
xcorners[:len(x)] = x-0.5*dx
xcorners[-1] = x[-1] + 0.5*dx
# make an energy range, for plots vs energy.
E = linspace(-20,20,10001)
#define color map that is transparent for low values, and dark blue for high values.
# weighted to show low probabilities well
cdic = {'red': [(0,0,0),(1,0,0)],
'green': [(0,0,0),(1,0,0)],
'blue': [(0,0.7,0.7),(1,0.7,0.7)],
'alpha': [(0,0,0),
(0.1,0.4,0.4),
(0.2,0.6,0.6),
(0.4,0.8,0.8),
(0.6,0.9,0.9),
(1,1,1)]}
cm_prob = matplotlib.colors.LinearSegmentedColormap('prob',cdic)
# To get eigenvalues, we need to set up a NxN matrix for the
# Schrodinger equation Hamiltonian. For the momentum operator
# (-hbar^2/(2*m) * d^2/dx^2) the typical central difference
# approximation will be used.
H = zeros((len(x),len(x)))
# set diagonal
H.ravel()[0::len(x)+1] = hbar*hbar/(mass*dx*dx)
H.ravel()[0::len(x)+1] += U
# set above and below diagonal
H.ravel()[1::len(x)+1] = -0.5*hbar*hbar/(mass*dx*dx)
H.ravel()[len(x)::len(x)+1] = -0.5*hbar*hbar/(mass*dx*dx)
# Right, the hamiltonian is set up, so let's just go ahead and
# diagonalize it, poink.
eigval, eigvec = eigh(H)
def doev(H, Emax):
lowE_idx = find(eigval<Emax)
figure()
for i in lowE_idx:
plot(x,eigvec[:,i], label='E = '+str(eigval[i]))
legend(fontsize=8)
micro = ((eigval > micro_e0)*(eigval < micro_e1))*1.0
print "microcanonical (E0 =",energy_microcanonical,", Delta =",0.5*range_microcanonical,") avg energy",
print sum(eigval*micro)/sum(micro)
canonical = exp(-eigval/temp_canonical)
canonical_avgE = sum(eigval*canonical)/sum(canonical)
print "canonical (T =",temp_canonical,") avg energy",
print canonical_avgE
# Boring level plot
fig = figure()
ax = axes()
plot(x,potential(x), linewidth=3)
for i in find(eigval<=13):
axhline(eigval[i], color=(0.5,0.5,0.5),linewidth=0.5,zorder=-1)
ylim(-8,9)
xlim(-2.1,1.7)
fig.get_axes()[0].xaxis.set_ticks([-2,-1,0,1])
xlabel("position $x$")
ylabel("potential $U(x)$")
fig.set_size_inches(3,3)
fig.patch.set_alpha(0)
savefig("quant_potential_eigval_lines"+figformat, **saveopts)
def levelplot(weights):
"""
Plot the potential with eigenstates' wavefunctions superimposed (shown).
weights: list fractions to multiply each eigenstate probability
(e.g., weight 0: do not show. weight 1: fully show)
name: filename to save to
"""
fig = figure()
ax = axes([0.08,0.1,0.73,0.89]) #([0.125,0.1,0.71,0.8])
plot(x,potential(x), linewidth=2, color='r', zorder=-1)
maxp = dx*3.5*amax(weights)
eigwidth = 0.2
for i in find(eigval<=9):
# Here, we plot the eigenfunctions as horizontal bars of varying darkness,
# with height set by the energy eigenvalue.
if weights[i] == 0: continue # don't plot levels with zero weight
pdist = eigvec[:,i]**2 * weights[i]
pdist.shape = (1,len(x))
extent = (amin(x)-0.5*dx, amax(x)+0.5*dx, eigval[i]-0.5*eigwidth, eigval[i]+0.5*eigwidth)
img = imshow(vstack((pdist,pdist)), cmap=cm_prob, extent=extent, interpolation='none', aspect='auto')
# Alternate code using pcolormesh doesn't work because of ugly edges.
# ycorners = vstack([
# [eigval[i]-0.5*eigwidth]*(len(x)+1),
# [eigval[i]+0.5*eigwidth]*(len(x)+1) ])
# pcolormesh(vstack([xcorners,xcorners]), ycorners, pdist, cmap=cm_prob)
clim(0,maxp)
ylim(-9,9)
xlim(-2.1,1.7)
fig.get_axes()[0].xaxis.set_ticks([-2,-1,0,1])
ax.xaxis.set_ticklabels([])
ax.yaxis.set_ticklabels([])
ax.xaxis.labelpad = 2
ax.yaxis.labelpad = -3
xlabel("position $x$")
ylabel("energy")
ax = axes([0.83,0.1,0.14,0.89], axisbg=(0.95,0.95,0.95))
ax.xaxis.set_ticks([])
ax.yaxis.set_ticklabels([])
ax.yaxis.set_ticks_position('right')
ylim(-9,9)
xlabel("states")
dos = E*0.0
for i,Elevel in enumerate(eigval):
# Here we sum up the density of states function
if Elevel > 20: continue # don't waste time with high levels
dos += exp(-4*((E-Elevel)/eigwidth)**2) * weights[i]
fill_betweenx(E, dos, linewidth=0, color=(0.2,0.2,0.76))
xlim(-0.05*max(dos),max(dos)*1.1)
fig.set_size_inches(3,3)
fig.patch.set_alpha(0)
levelplot(ones(len(eigval)))
savefig("quant_potential_eigval_pdists"+figformat, **saveopts)
levelplot(micro)
sca(gcf().axes[0])
axhspan(micro_e0, micro_e1, color=(0.7,1,0.7),zorder=-2)
sca(gcf().axes[1])
axhspan(micro_e0, micro_e1, color=(0.7,1,0.7),zorder=-2)
savefig("quant_potential_eigval_pdists_micro"+figformat, **saveopts)
levelplot(canonical)
sca(gcf().axes[0])
annotate("$\\langle E\\rangle$", (-0.5,canonical_avgE),
textcoords=None,verticalalignment='top',color=(0,0.4,0))
axhline(canonical_avgE, linestyle='dotted', linewidth=1,color=(0,0.4,0))
annotate('',(1.2,7.-temp_canonical),(1.2,7.),
arrowprops = {'arrowstyle':'<->'})
text(1.15,7.-0.5*temp_canonical,'$kT$',
horizontalalignment='right',verticalalignment='center')
sca(gcf().axes[1])
axhline(canonical_avgE, linestyle='dotted', linewidth=1,color=(0,0.4,0))
fill_betweenx(E, exp(-E/temp_canonical), linewidth=0, color=(0.7,1,0.7),zorder=-2) # green exponential
savefig("quant_potential_eigval_pdists_canonical"+figformat, **saveopts)
# Position expectation values
figure()
pdist = zeros(len(x))
for i,p in enumerate(micro): pdist += p*eigvec[:,i]**2
if any(micro):
plot(x, pdist/sum(micro)/dx, label='microcanonical')
pdist = zeros(len(x))
for i,p in enumerate(canonical): pdist += p*eigvec[:,i]**2
plot(x, pdist/sum(canonical)/dx, label='canonical', color='g')
xlim(-2.1,1.7)
fig.get_axes()[0].xaxis.set_ticks([-2,-1,0,1])
xlabel("position $x$")
ylabel("PDF of position $P(x)$")
legend()
savefig("quant_position_pdf"+figformat, **saveopts)
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
| This file is made available under the Creative Commons CC0 1.0 Universal Public Domain Dedication. | |
| The person who associated a work with this deed has dedicated the work to the public domain by waiving all of their rights to the work worldwide under copyright law, including all related and neighboring rights, to the extent allowed by law. You can copy, modify, distribute and perform the work, even for commercial purposes, all without asking permission.
http://creativecommons.org/publicdomain/zero/1.0/deed.enCC0Creative Commons Zero, Public Domain Dedicationfalsefalse |
Captions
Add a one-line explanation of what this file represents
Items portrayed in this file
depicts
30 October 2013
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 21:51, 30 October 2013 | 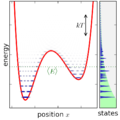 | 900 × 900 (78 KB) | Nanite | User created page with UploadWizard |
File usage
The following 2 pages use this file:
Global file usage
The following other wikis use this file:
- Usage on fa.wikipedia.org
- Usage on fr.wikipedia.org
Metadata
This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.
If the file has been modified from its original state, some details may not fully reflect the modified file.
| Horizontal resolution | 118.11 dpc |
|---|---|
| Vertical resolution | 118.11 dpc |
