File:Academ scale ratio cos 30deg.svg
Size of this PNG preview of this SVG file: 625 × 500 pixels. Other resolutions: 300 × 240 pixels | 600 × 480 pixels | 960 × 768 pixels | 1,280 × 1,024 pixels | 2,560 × 2,048 pixels.
Original file (SVG file, nominally 625 × 500 pixels, file size: 4 KB)
 | This is a file from the Wikimedia Commons. Information from its description page there is shown below. Commons is a freely licensed media file repository. You can help. |
Summary
| Description |
English: The right triangles ABC and ACH are similar, because they are halves of equilateral triangles. The reproduction of the first triangle into the second one multiplies its area by 3/ 4. Hence the value of the scale ratio, also equal to the cosine of 30 degrees. The similarity that transforms the first triangle into the second triangle has a fixed point, that is the only point equal to its image under the similarity. This point is A, it is called the center of the similarity. And the angle of this direct similarity is – 30 degrees modulo 360 degrees.
Remark. The writing 3/ 4 is a fraction, the ratio of the areas is a rational number. No fraction equals exactly the scale ratio; that is irrational. Français : Les triangles rectangles ABC et ACH sont semblables, parce que ce sont des moitiés de triangles équilatéraux. La reproduction du premier triangle en le second multiplie son aire par 3/ 4. D’où la valeur de l’échelle de reproduction, aussi égale au cosinus de 30 degrés. La similitude qui transforme le premier triangle en le second possède un point invariant, c’est le seul point égal à son image par la similitude. Ce point est A, on l’appelle le centre de la similitude. Et l’angle de cette similitude directe est – 30 degrés modulo 360 degrés. Remarque. L’écriture 3/ 4 est une fraction, le rapport des aires est un nombre rationnel. Aucune fraction n’est exactement égale à l’échelle de reproduction, qui est est irrationnelle. |
| Date | |
| Source | Own work |
| Author | Yves Baelde |
| Other versions |
Published in France in “Souci d’exactitude” (Yves Baelde), Bulletin de l’APMEP n° 401, december 1995 (p.877). Other version: File:Academ_scale_ratio_tan_60deg.svg |
This /Baelde was created with a text editor.
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.
- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 15:07, 18 September 2011 | | 625 × 500 (4 KB) | Baelde | the classical formula a² + b² = c² holds with the new notations, the red and green lines are more shiny, etc. |
| 09:48, 23 May 2010 | 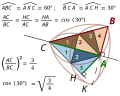 | 450 × 360 (3 KB) | Baelde | {{Information |Description={{en|1=The image shows the value of ''cos''(30°). The triangle BCK is equilateral. The orthogonal projection onto (KC) transforms the midpoint A of [BK] into H. A tiling fills BCK with eight right triangles, congruent one |
File usage
The following page uses this file:
