File:01-100-Eck-Quadratrix.svg

Original file (SVG file, nominally 631 × 621 pixels, file size: 429 KB)
| This is a file from the Wikimedia Commons. Information from its description page there is shown below. Commons is a freely licensed media file repository. You can help. |
Contents
Summary
| Description01-100-Eck-Quadratrix.svg |
Deutsch: 100-Eck, exakte Konstruktion mithilfe der Quadratrix des Hippias als zusätzliches Hilfsmittel
|
| Date | |
| Source | Own work |
| Author | Petrus3743 |
| Other versions |
 Hectogon, exact construction using the quadratrix of Hippias as an additional aid, animation |
| SVG development InfoField |
Konstruktion
Das regelmäßige 100-Eck ist unter alleiniger Verwendung der klassischen Konstruktionsmittel Zirkel und Lineal nicht konstruierbar. Ein zusätzliches Hilfsmittel zur Dreiteilung beliebiger Winkel reicht ebenfalls nicht aus. Nimmt man jedoch ein zusätzliches Hilfsmittel, das die Teilung des 90-Grad-Winkels in 
Vorüberlegungen
- Um von einem regelmäßigen 100-Eck den Zentriwinkel
mithilfe der Quadratrix des Hippias zu finden, ist zuerst eine sogenannte Hilfsstrecke zu konstruieren, deren Gesamtlänge
gleich langer Teile entspricht, aber die Abschnitte aus den Radien
und
(Summe
) zusammengesetzt sind.
- Der Zentriwinkel des 100-Ecks ergibt sich aus
aber die Quadratrix des Hippias unterteilt nur die Winkel ab
bis
in gleich große Winkel. Daraus folgt, ein Hundertstel der Strecke
kann nur ein Hundertstel des Winkels
erzielen. Deshalb wird wegen der Berechnung des Zentriwinkels
aus dem Umkreis mit seinen
das Vierfache eines Hundertstel, d. h. der Teilungspunkt
der Strecke
zur Konstruktion des Zentriwinkels
genutzt.
- Es ist nicht erforderlich die Strecke
in
einzelne, gleich lange Teile zu unterteilen, denn man benötigt davon nur die Länge von
Teilen. Des Weiteren ist es bei einer sehr hohe Anzahl der Teilungen (sehr kleine Zirkelöffnung für z. B.
Teil) vorteilhaft, den Durchmesser des Umkreises als Summe von
gleich langen Teilen festzulegen. Aufgrund dessen wird im Folgenden die sogenannte Hilfsstrecke nur aus
Radien – Vielfaches eines Hundertstel – zusammengesetzt.
Quadratrix des Hippias als zusätzliches Hilfsmittel

Nach dem Zeichen des Kreises um dessen Mittelpunkt 



mit
Es geht weiter mit dem Einzeichnen des Durchmessers 





Es folgt die Festlegung der sogenannten Hilfsstrecke mit den Radien 






































Nach dem Abtragen der noch fehlenden Seitenlängen 

Siehe auch
Einzelnachweise
- ↑ Hans-Wolfgang Henn: Elementare Geometrie und Algebra. Verlag Vieweg+Teubner 2003, S. 45–48 Die Quadratur des Kreises (Auszug Google), abgerufen am 23. März 2018
- ↑ Horst Hischer: Mathematik in der Schule 32 (1994) 5, Geschichte der Mathematik als didaktischer Aspekt (2). Lösung klassischer Probleme, ab Seite 279, abgerufen am 23. März 2018
Licensing
- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.
Captions
Items portrayed in this file
depicts
22 March 2018
image/svg+xml
a9f639e6ed9187c3466bc80b75ffc3e40e497f3e
439,793 byte
621 pixel
631 pixel
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 12:19, 22 March 2018 | 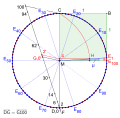 | 631 × 621 (429 KB) | Petrus3743 | User created page with UploadWizard |
File usage
The following page uses this file:
Global file usage
The following other wikis use this file:
- Usage on es.wikipedia.org
Metadata
This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.
If the file has been modified from its original state, some details may not fully reflect the modified file.
| Width | 17.81790155977665cm |
|---|---|
| Height | 17.513611020805136cm |


