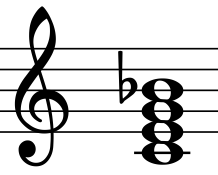Vogel's Tonnetz
Vogel's Tonnetz is a graphical and mathematical representation of the scale range of just intonation, introduced by German music theorist Martin Vogel 1976 in his book Die Lehre von den Tonbeziehungen (English: On the Relations of Tone, 1993). The graphical representation is based on Euler's Tonnetz, adding a third dimension for just sevenths to the two dimensions for just fifths and just thirds. It serves to illustrate and analyze chords and their relations. The four-dimensional mathematical representation including octaves allows the Evaluation of the congruency of harmonics of chords depending on the tonal material. It can thus also serve to determine the optimal tonal material for a certain chord.
The graphical representation
[edit]The graphical representation of Vogel's Tonnetz is limited to the three dimensions for fifths, thirds, and seventh. In this representation tones separated by one or several octaves are depicted on the same nodes. The illustration shows the chord which is the most frequent 4-note chord in western music: the dominant seventh. In Euler's Tonnetz the B-flat is constructed from fifths and thirds. In Vogel's Tonnetz it is given as a just harmonic seventh.
-
Seventh chord
-
Representation in Euler's Tonnetz
-
Representation in Vogel's Tonnetz
The representation of this chord in Vogel's three-dimensional Tonnetz makes its statistical dominance much more plausible than its representation in Euler's two-dimensional Tonnetz: There is a distinct reference note (C), and all other notes are linked to this reference note via simple one-step intervals in this Tonnetz.
The mathematical representation
[edit]The mathematical representation of Vogel's Tonnetz is four-dimensional, considering also octaves. Each tone is represented by a quadruple of numbers specifying how many octaves, "fifths", "thirds", and "seventh" are needed to reach that tone in the Tonnetz (where the terms "fifths", "thirds", and "seventh" denote the prime numbers 3, 5, and 7, instead of the intervals 3/2, 5/4 and 7/4). The C-major seventh chord with the notes c', e', g', and b-flat' could (with reference to C)be represented by the numbers 4, 5, 6, and 7. This corresponds to the quadruple (2,0,0,0), (0,0,1,0), (1,1,0,0), and (0,0,0,1). The quadruple notations represents the prime decomposition of the numbers that are needed to describe the chord, limited to the first four prime numbers.
Vogel adopts the harmonic dualism of Arthur von Oettingen, with major and minor chords being mirror images of each other. This view is complemented by a quantitative computation of consonance (or rather dissonance) values.

For this purpose Vogel introduces virtual reference tones that are not necessarily part of the chord. These reference tones are chosen such that all chord tones have integer relations to these reference tones. For each chord there exists a lower and an upper reference tone, with all chord tones being integer multiples of the frequency of the lower reference tone and integer fractions of the frequency of the upper reference tone. In quadruple notation there are only positive (or zero) values if the chord is related to the lower reference tone, and only negative (or zero) values if the chord is related to the higher reference tone.
To get a single numerical value describing the complexity of a chord, Vogel builds a weighted sum of the quadruples describing the notes of the chord. He suggests the weights 1, 3, 5, and 7 for the prime numbers 2, 3, 5, and 7. Vogel rejects the more obvious variant where prime number 2 is weighted with 2 because it leads to results that in his opinion do not comply with the perception of musically skilled listeners. Finally, the weighted sum is divided by the number of tones of the chord. This computation is done for both the higher and the lower reference tone. Depending on which of those two values is smaller, the chord is then labeled as "Oberklang" or "Unterklang" ("upper chord", if reference to the lower reference note, or "lower chord", if referenced to the upper reference note).
The C major chord c’-e’-g’ could, for instance, be referenced to C. All three notes of the triad can be represented as integer multiples of the frequency of this reference tone (4, 5, and 6). The prime decomposition yields 2·2,5,2·3. Applying the weights suggested by Vogel one obtains a so-called consonance value of (1+1+5+1+3)/3 = 11/3 = 3.67. The same chord may also be referenced to b’’’’: this upper reference tone has 15 times the frequency of c’, 12 times the frequency of e’ and ten times the frequency of g’. The prime decomposition yields3·5,2·2·3,2·5. The consonance value computes to (3+5+1+1+3+1+5)/3 = 19/3 = 6,33. As the consonance value for the lower reference tone is better (smaller), the c major chord c’-e’-g’ is defined to be an upper chord referenced to C. The consonance value of the c minor chord c’-es’-g’ is identical. It is, however, reference to the upper reference tone of this chord, g’’’. In consequence, Vogel rejects the naming of this chord as C minor as its reference note is not C but G. He calls it "G lower chord".
Vogel suggests a specific notation for upper and lower chords. The notation starts by denoting the reference tone in lower case. Upper chords are marked by an "O" (Oberklang) and are denoted from left to right, lower chords are marked by a "U" (Unterklang) and are denoted from right to left. The C major chord is denoted as cO, the C minor chord is denoted as Ug. Additional symbols for additional notes (7 for adding an upper or lower seventh) are added to the left or to the right, depending on whether it is an upper or a lower chord. The C7 chord depicted above would be denoted as cO7.
In addition to the calculation of consonance values for single chords, Vogel suggests a computation of the consonance of chord transitions. When transiting from an n-note chord to an m-note chord all N·M note-to-note transitions are evaluated via prime decomposition and weighted sum, and a mean value for all these transitions is computed. Vogel also suggest to compute a consonance value for an entire piece of music, taking into account a central reference point similar to a final.
Consonance and the congruency of harmonics
[edit]The consonance value calculated with Vogel's formula should rather be termed dissonance value, because with increasing dissonance of a chord or interval its value increases. Vogel did not claim to predict consonance judgments of today's listeners. A close relation of Vogel's consonance values with consonance judgments is in deed not to be expected. Firstly, consonance judgments correlate strongly with familiarity judgments.[1] Secondly, major and minor are attributed emotional values by today's Western listeners (minor being perceived as expressing sadness). Thirdly, his formula considers only the congruency of harmonics, but not the congruency of combination tones. It would be more cautious to say that Vogel's formula correlates with the congruency of harmonics, expressing in how far the harmonics of a chord fit together or not.
The range of the validity of the formula is in addition limited by the limits of hearing. A just octave cannot be discriminated from an octave that is mistuned by a schisma (a mistuning of about 2 cent). The perceptual limit for the frequency difference of complex tones is about 0.25% (4 cent).[2] Vogel's consonance formula yields a consonance value of (1·1+0·3+0·5+0·7)/2 = 0.5 for the just octave (1,0,0,0), and a values of (14·1+8·3+1·5+0·7)/2 = 43/2 = 21.5 for the octave mistuned by a schisma (-14,8,1,0).
Consequences for the selection of tones
[edit]
Vogel's consonance formula can help to decide, which tones of the Tonnetz should be taken for a certain chord. The consonance value of the seventh chord in Euler's Tonnetz (see figure above) is 8.5. In Vogel's Tonnetz one could select the same tones, resulting in the same consonance value. If one, however, decides to select the just seventh, the consonance value improves to 4.5. Hence, according to Vogel, the seventh chord using a just seventh is to be preferred over a seventh chord where the seventh is built from fifth and thirds.
Compositional consequences
[edit]Vogel claims that his formula entails also compositional consequences. If one wants a chord to be consonant, major chords should be composed such that thirds and sevenths are set in a high register. Minor chords, however, would have to be set the other way round, with thirds and sevenths being set in a low register. This is by no means compatible with the compositional practice of the last centuries (with perhaps the exception of the Tristan chord, see below). In consequence, minor chords set along Vogel's composition rules sound unfamiliar. They exhibit, however, a better congruency of harmonics than their classical variants. The left-hand of the two C minor chords in the adjoining figure is composed in the classical way, with the third being set in a high register. The consonance value for this chord is 4.33. The right-hand minor chord features a low third. It sounds unfamiliar. Its consonance value is, however, much lower (3.0), and the congruency of its harmonics is much better.
Limiting the theory to the prime numbers 2, 3, 5 and 7
[edit]Vogel considers the theoretically infinite four-dimensional space of tones of his Tonnetz as complete; no further dimensions are needed for higher prime numbers. According to his theory, consonance results from the congruency of harmonics. The prime number 11 and any other higher prime number can not lead to any perception of congruency, as the inner ear separates only the first eight to ten partials.[2] The eleventh partial may be audible and discriminable from the tenth or twelfth partial if isolated via techniques such as flageolet. If presented as part of a complex tone comprising also the adjoining partials these partials would fuse together, and a congruency with the partial of another note could no longer be detected. It might be interesting to test whether it is possible to detect harmonic congruency for higher prime numbers for instruments with odd partials, as the distances between partials are higher in these instruments. With training it might be possible to detect consonance up to prime number 17 or even 19.
The half-diminished seventh chord in Vogel's Tonnetz
[edit]

The Tristan chord is a historically important chord in Richard Wagner's opera Tristan and Isolde. Its role in functional harmony cannot clearly be determined. It is considered to be tonally unsettled and extremely chromatic.[3]
In Vogel's Tonnetz this chord appears to be the dual counterpiece of a major seventh chord. This interpretation is strengthened by the observation that this G-sharp minor chord with an added lower seventh (E-sharp or F is a seventh below the reference of this G-sharp minor chord, the D-sharp) resolves in an E major chord with an added upper seventh (see also the adjoining animated figure). In addition, Wagner's way to set this chord is compatible with this view, with the third (B) and the seventh (F or E-sharp) set in a low register. In Vogel's notation one would note this chord as 7Ud♯, as the reference note of the G-sharp minor chord is the D-sharp.
It is not very likely that Vogel's notation for minor chords will win recognition. It would require that a C minor chord is denoted as Ug, as lower chord under g. A compromise notation could be to denote the Tristan chord as G♯m/F, i.e., as a G-sharp minor chord with an F in the bass.
The "explanation" of the Tristan chord in Vogel's Tonnetz as a well-composed counter-piece of a major seventh chord cannot be compared to an "explanation" in the scope of functional harmony. Both types of explanations cannot really explain why certain chords and chord sequences have established themselves in musical history. Functional harmony focuses on the relation of a chord to the prevailing tonality. In consequence, it cannot explain chord progressions found in late-romantic music where there is no longer a continuous tonality present. In contrast, Vogel's theory focuses more on the congruency of the notes of a single chord, or with the notes of the preceding or subsequent chord than on the role of this chord in the context of a prevailing tonality. Vogel's analysis reveals that the Tristan chord is by no means an attack on the tonal system as such but that it is part of it exactly as its counterpart, the major seventh chord.
A similar chord is also often used by jazz musicians. There it is commonly notated as a half-diminished seventh chord. The Tristan chord could hence be noted as Fm7 b5). This way to describe this chord misses its relation to a G-sharp minor chord. It results from the practice to describe chords starting from their lowest note. According to Vogel this is appropriate for upper chords, but not for lower chords. Lower chords should be described top-down instead of bottom-up. The principle of starting with the lowest note is not consequently observed in other situations, such as with inverted chords. A C major chord in its first inversion is not typically described as an E minor chord with altered fifth (Em+5).
Reception
[edit]Vogel's Tonnetz resorts on a theory (Euler's Tonnetz) that is more than 100 years older than the presently dominating functional harmony. Vogel's Tonnetz and functional harmony are not in conflict with each other. On the contrary, they can be seen as complementing each other: While Vogel's theory focuses on local relations of tones and chords, functional harmony considers the global role of a chord in the context of the entire piece of music. However, the prevalence of functional harmony and the peculiarities of Vogel's notation hamper the general reception. Vogel's consonance formula has only recently been tested empirically.[1] Kaernbach suggests a simplified notation: writing always from left to right, using capital letters for the reference tones (avoiding confusions with the convention to use lowercase letters for minor chords), and using a triangular symbol (▲ and ▼) to denote upper and lower chords. The beginning of the prelude of Tristan and Isolde could then be denoted as D♯▼7 → E▲7.[4]
Literature
[edit]- Martin Vogel: Der Tristanakkord und die Krise der modernen Harmonielehre. Düsseldorf 1962.
- Martin Vogel: Die Lehre von den Tonbeziehungen. Bonn 1976.
- Martin Vogel: On the Relation of Tone. Bonn 1993.
References
[edit]- ^ a b Agnieszka Karas, Christian Kaernbach: Putting Martin Vogel to test: An attempt to evaluate a musical theory. In U. Ansorge et al. (Hrsg.): Beiträge zur 55. Tagung experimentell arbeitender Psychologen.[permanent dead link] (PDF; 11,3 MB) Pabst Science Publishers, Lengerich, 2013, S. 43.
- ^ a b Christian Kaernbach, Christian Bering: Exploring the temporal mechanism involved in the pitch of unresolved harmonics. In: Journal of the Acoustical Society of America. Vol. 110, 2001, S. 1039-1048 (PDF).
- ^ Ernst Kurth: Romantische Harmonik und ihre Krise in Wagners „Tristan“, Bern 1920.
- ^ Christian Kaernbach: Honoring Martin Vogel – Champion of just intonation in music. In U. Ansorge et al. (Hrsg.): Beiträge zur 55. Tagung experimentell arbeitender Psychologen.[permanent dead link] (PDF; 11,3 MB) Pabst Science Publishers, Lengerich, 2013, S. 43.