Cyclotruncated simplicial honeycomb

In geometry, the cyclotruncated simplicial honeycomb (or cyclotruncated n-simplex honeycomb) is a dimensional infinite series of honeycombs, based on the symmetry of the ${\tilde {A}}_{n}$ affine Coxeter group. It is given a Schläfli symbol t_0,1{3^[n+1]}, and is represented by a Coxeter-Dynkin diagram as a cyclic graph of n+1 nodes with two adjacent nodes ringed. It is composed of n-simplex facets, along with all truncated n-simplices.

It is also called a Kagome lattice in two and three dimensions, although it is not a lattice.

In n-dimensions, each can be seen as a set of n+1 sets of parallel hyperplanes that divide space. Each hyperplane contains the same honeycomb of one dimension lower.

In 1-dimension, the honeycomb represents an apeirogon, with alternately colored line segments. In 2-dimensions, the honeycomb represents the trihexagonal tiling, with Coxeter graph . In 3-dimensions it represents the quarter cubic honeycomb, with Coxeter graph filling space with alternately tetrahedral and truncated tetrahedral cells. In 4-dimensions it is called a cyclotruncated 5-cell honeycomb, with Coxeter graph , with 5-cell, truncated 5-cell, and bitruncated 5-cell facets. In 5-dimensions it is called a cyclotruncated 5-simplex honeycomb, with Coxeter graph , filling space by 5-simplex, truncated 5-simplex, and bitruncated 5-simplex facets. In 6-dimensions it is called a cyclotruncated 6-simplex honeycomb, with Coxeter graph , filling space by 6-simplex, truncated 6-simplex, bitruncated 6-simplex, and tritruncated 6-simplex facets.

n	${\tilde {A}}_{n}$	Name Coxeter diagram	Vertex figure	Image and facets
1	${\tilde {A}}_{1}$	Apeirogon		Yellow and cyan line segments
2	${\tilde {A}}_{2}$	Trihexagonal tiling	Rectangle	With yellow and blue equilateral triangles, and red hexagons
3	${\tilde {A}}_{3}$	quarter cubic honeycomb	Elongated triangular antiprism	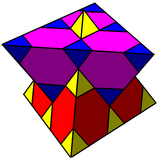With yellow and blue tetrahedra, and red and purple truncated tetrahedra
4	${\tilde {A}}_{4}$	Cyclotruncated 5-cell honeycomb	Elongated tetrahedral antiprism	5-cell, truncated 5-cell, bitruncated 5-cell
5	${\tilde {A}}_{5}$	Cyclotruncated 5-simplex honeycomb		5-simplex, truncated 5-simplex, bitruncated 5-simplex
6	${\tilde {A}}_{6}$	Cyclotruncated 6-simplex honeycomb		6-simplex, truncated 6-simplex, bitruncated 6-simplex, tritruncated 6-simplex
7	${\tilde {A}}_{7}$	Cyclotruncated 7-simplex honeycomb		7-simplex, truncated 7-simplex, bitruncated 7-simplex
8	${\tilde {A}}_{8}$	Cyclotruncated 8-simplex honeycomb		8-simplex, truncated 8-simplex, bitruncated 8-simplex, tritruncated 8-simplex, quadritruncated 8-simplex

Projection by folding

The cyclotruncated (2n+1)- and 2n-simplex honeycombs and (2n-1)-simplex honeycombs can be projected into the n-dimensional hypercubic honeycomb by a geometric folding operation that maps two pairs of mirrors into each other, sharing the same vertex arrangement:

${\tilde {A}}_{3}$		${\tilde {A}}_{5}$		${\tilde {A}}_{7}$		${\tilde {A}}_{9}$		${\tilde {A}}_{11}$		...
${\tilde {A}}_{2}$		${\tilde {A}}_{4}$		${\tilde {A}}_{6}$		${\tilde {A}}_{8}$		${\tilde {A}}_{10}$		...
		${\tilde {A}}_{3}$		${\tilde {A}}_{5}$		${\tilde {A}}_{7}$		${\tilde {A}}_{9}$		...
${\tilde {C}}_{1}$		${\tilde {C}}_{2}$		${\tilde {C}}_{3}$		${\tilde {C}}_{4}$		${\tilde {C}}_{5}$		...

See also

• Hypercubic honeycomb
• Alternated hypercubic honeycomb
• Quarter hypercubic honeycomb
• Simplectic honeycomb
• Omnitruncated simplicial honeycomb

References

• George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
• Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
• Norman Johnson Uniform Polytopes, Manuscript (1991)
• Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]

Fundamental convex regular and uniform honeycombs in dimensions 2–9
Space	Family	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde {E}}_{n-1}$
E2	Uniform tiling	0[3]	δ3	hδ3	qδ3	Hexagonal
E3	Uniform convex honeycomb	0[4]	δ4	hδ4	qδ4
E4	Uniform 4-honeycomb	0[5]	δ5	hδ5	qδ5	24-cell honeycomb
E5	Uniform 5-honeycomb	0[6]	δ6	hδ6	qδ6
E6	Uniform 6-honeycomb	0[7]	δ7	hδ7	qδ7	222
E7	Uniform 7-honeycomb	0[8]	δ8	hδ8	qδ8	133 • 331
E8	Uniform 8-honeycomb	0[9]	δ9	hδ9	qδ9	152 • 251 • 521
E9	Uniform 9-honeycomb	0[10]	δ10	hδ10	qδ10
E10	Uniform 10-honeycomb	0[11]	δ11	hδ11	qδ11
En-1	Uniform (n-1)-honeycomb	0[n]	δn	hδn	qδn	1k2 • 2k1 • k21