Conflict-driven clause learning

In computer science, conflict-driven clause learning (CDCL) is an algorithm for solving the Boolean satisfiability problem (SAT). Given a Boolean formula, the SAT problem asks for an assignment of variables so that the entire formula evaluates to true. The internal workings of CDCL SAT solvers were inspired by DPLL solvers. The main difference between CDCL and DPLL is that CDCL's backjumping is non-chronological.

Conflict-driven clause learning was proposed by Marques-Silva and Karem A. Sakallah (1996, 1999) and Bayardo and Schrag (1997).

Background

Boolean satisfiability problem

Main article: Boolean satisfiability problem

The satisfiability problem consists in finding a satisfying assignment for a given formula in conjunctive normal form (CNF).

An example of such a formula is:

( (not A) or (not C) )   and   (B or C),

or, using a common notation:

$(\lnot A\lor \lnot C)\land (B\lor C)$

where A,B,C are Boolean variables, $\lnot A$, $\lnot C$, $B$, and $C$ are literals, and $\lnot A\lor \lnot C$ and $B\lor C$ are clauses.

A satisfying assignment for this formula is e.g.:

$A=\mathrm {False} ,B=\mathrm {False} ,C=\mathrm {True}$

since it makes the first clause true (since $\lnot A$ is true) as well as the second one (since $C$ is true).

This examples uses three variables (A, B, C), and there are two possible assignments (True and False) for each of them. So one has $2^{3}=8$ possibilities. In this small example, one can use brute-force search to try all possible assignments and check if they satisfy the formula. But in realistic applications with millions of variables and clauses brute force search is impractical. The responsibility of a SAT solver is to find a satisfying assignment efficiently and quickly by applying different heuristics for complex CNF formulas.

Unit clause rule (unit propagation)

Main article: Unit propagation

If a clause has all but one of its literals or variables evaluated at False, then the free literal must be True in order for the clause to be True. For example, if the below unsatisfied clause is evaluated with $A=\mathrm {False}$ and $B=\mathrm {False}$ we must have $C=\mathrm {True}$ in order for the clause $(A\lor B\lor C)$ to be true.

The iterated application of the unit clause rule is referred to as unit propagation or Boolean constraint propagation (BCP).

Resolution

Main article: Resolution (logic)

Consider two clauses $(A\lor B\lor C)$ and $(\neg C\lor D\lor \neg E)$. The clause $(A\lor B\lor D\lor \neg E)$, obtained by merging the two clauses and removing both $\neg C$ and $C$, is called the resolvent of the two clauses.

Algorithm

Conflict-driven clause learning works as follows.

1. Select a variable and assign True or False. This is called decision state. Remember the assignment.
2. Apply Boolean constraint propagation (unit propagation).
3. Build the implication graph.
4. If there is any conflict
   1. Find the cut in the implication graph that led to the conflict
   2. Derive a new clause which is the negation of the assignments that led to the conflict
   3. Non-chronologically backtrack ("back jump") to the appropriate decision level, where the first-assigned variable involved in the conflict was assigned
5. Otherwise continue from step 1 until all variable values are assigned.

Example

A visual example of CDCL algorithm:

• 
  At first pick a branching variable, namely x1. A yellow circle means an arbitrary decision.
• 
  Now apply unit propagation, which yields that x4 must be 1 (i.e. True). A gray circle means a forced variable assignment during unit propagation. The resulting graph is called an implication graph.
• 
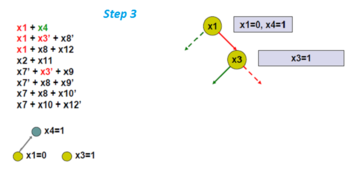
  Arbitrarily pick another branching variable, x3.
• 
  Apply unit propagation and find the new implication graph.
• 
  Here the variables x8 and x12 are forced to be 0 and 1, respectively.
• 
  Pick another branching variable, x2.
• 
  Find implication graph.
• 
  Pick another branching variable, x7.
• 
  Find implication graph.
• 
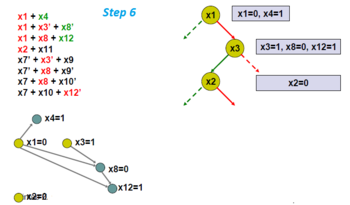
  Found a conflict!
• 
  Find the cut that led to this conflict. From the cut, find a conflicting condition.
• 
  Take the negation of this condition and make it a clause.
• 
  Add the conflict clause to the problem.
• 
  Non-chronological back jump to appropriate decision level, which in this case is the second highest decision level of the literals in the learned clause.
• 
  Back jump and set variable values accordingly.

Completeness

DPLL is a sound and complete algorithm for SAT. CDCL SAT solvers implement DPLL, but can learn new clauses and backtrack non-chronologically. Clause learning with conflict analysis affects neither soundness nor completeness. Conflict analysis identifies new clauses using the resolution operation. Therefore, each learnt clause can be inferred from the original clauses and other learnt clauses by a sequence of resolution steps. If cN is the new learnt clause, then ϕ is satisfiable if and only if ϕ ∪ {cN} is also satisfiable. Moreover, the modified backtracking step also does not affect soundness or completeness, since backtracking information is obtained from each new learnt clause.

Applications

The main application of CDCL algorithm is in different SAT solvers including:

• MiniSAT
• Zchaff SAT
• Z3
• Glucose
• ManySAT etc.

The CDCL algorithm has made SAT solvers so powerful that they are being used effectively in several real world application areas like AI planning, bioinformatics, software test pattern generation, software package dependencies, hardware and software model checking, and cryptography.

Related algorithms

Related algorithms to CDCL are the Davis–Putnam algorithm and DPLL algorithm. The DP algorithm uses resolution refutation and it has potential memory access problem. Whereas the DPLL algorithm is OK for randomly generated instances, it is bad for instances generated in practical applications. CDCL is a more powerful approach to solve such problems in that applying CDCL provides less state space search in comparison to DPLL.

• 
  DPLL: no learning and chronological backtracking.
• 
  CDCL: conflict-driven clause learning and non – chronological backtracking.

References

• Martin Davis; Hilary Putnam (1960). "A Computing Procedure for Quantification Theory". J. ACM. 7 (3): 201–215. doi:10.1145/321033.321034. S2CID 31888376.
• Martin Davis; George Logemann; Donald Loveland (Jul 1962). "A machine program for theorem-proving". Communications of the ACM. 5 (7): 394–397. doi:10.1145/368273.368557. hdl:2027/mdp.39015095248095. S2CID 15866917.
• Matthew W. Moskewicz; Conor F. Madigan; Ying Zhao; Lintao Zhang; Sharad Malik (2001). "Chaff: engineering an efficient SAT solver" (PDF). Proc. 38th Ann. Design Automation Conference (DAC). pp. 530–535.
• Lintao Zhang; Conor F. Madigan; Matthew H. Moskewicz; Sharad Malik (2001). "Efficient conflict driven learning in a boolean satisfiability solver" (PDF). Proc. IEEE/ACM Int. Conf. on Computer-aided design (ICCAD). pp. 279–285.
• Presentation – "SAT-Solving: From Davis-Putnam to Zchaff and Beyond" by Lintao Zhang. (Several pictures are taken from his presentation)