Vector (mathematics and physics)
In mathematics and physics, vector is a term that refers to quantities that cannot be expressed by a single number (a scalar), or to elements of some vector spaces. They have to be expressed by both magnitude and direction.
Historically, vectors were introduced in geometry and physics (typically in mechanics) for quantities that have both a magnitude and a direction, such as displacements, forces and velocity. Such quantities are represented by geometric vectors in the same way as distances, masses and time are represented by real numbers.
The term vector is also used, in some contexts, for tuples, which are finite sequences (of numbers or other objects) of a fixed length.
Both geometric vectors and tuples can be added and scaled, and these vector operations led to the concept of a vector space, which is a set equipped with a vector addition and a scalar multiplication that satisfy some axioms generalizing the main properties of operations on the above sorts of vectors. A vector space formed by geometric vectors is called a Euclidean vector space, and a vector space formed by tuples is called a coordinate vector space.
Many vector spaces are considered in mathematics, such as extension fields, polynomial rings, algebras and function spaces. The term vector is generally not used for elements of these vector spaces, and is generally reserved for geometric vectors, tuples, and elements of unspecified vector spaces (for example, when discussing general properties of vector spaces).
Vectors in Euclidean geometry
[edit]
In mathematics, physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector[1] or spatial vector[2]) is a geometric object that has magnitude (or length) and direction. Euclidean vectors can be added and scaled to form a vector space. A vector quantity is a vector-valued physical quantity, including units of measurement and possibly a support, formulated as a directed line segment. A vector is frequently depicted graphically as an arrow connecting an initial point A with a terminal point B,[3] and denoted by
A vector is what is needed to "carry" the point A to the point B; the Latin word vector means "carrier".[4] It was first used by 18th century astronomers investigating planetary revolution around the Sun.[5] The magnitude of the vector is the distance between the two points, and the direction refers to the direction of displacement from A to B. Many algebraic operations on real numbers such as addition, subtraction, multiplication, and negation have close analogues for vectors,[6] operations which obey the familiar algebraic laws of commutativity, associativity, and distributivity. These operations and associated laws qualify Euclidean vectors as an example of the more generalized concept of vectors defined simply as elements of a vector space.
Vectors play an important role in physics: the velocity and acceleration of a moving object and the forces acting on it can all be described with vectors.[7] Many other physical quantities can be usefully thought of as vectors. Although most of them do not represent distances (except, for example, position or displacement), their magnitude and direction can still be represented by the length and direction of an arrow. The mathematical representation of a physical vector depends on the coordinate system used to describe it. Other vector-like objects that describe physical quantities and transform in a similar way under changes of the coordinate system include pseudovectors and tensors.[8]Vector quantities
[edit]In the natural sciences, a vector quantity (also known as a vector physical quantity, physical vector, or simply vector) is a vector-valued physical quantity.[9][10] It is typically formulated as the product of a unit of measurement and a vector numerical value (unitless), often a Euclidean vector with magnitude and direction. For example, a position vector in physical space may be expressed as three Cartesian coordinates with SI unit of meters.
In physics and engineering, particularly in mechanics, a physical vector may be endowed with additional structure compared to a geometrical vector.[11] A bound vector is defined as the combination of an ordinary vector quantity and a point of application or point of action.[9] [12] Bound vector quantities are formulated as a directed line segment, with a definite initial point besides the magnitude and direction of the main vector.[9][11] For example, a force on the Euclidean plane has two Cartesian components in SI unit of newtons and an accompanying two-dimensional position vector in meters, for a total of four numbers on the plane (and six in space).[13][14][12] A simpler example of a bound vector is the translation vector from an initial point to an end point; in this case, the bound vector is an ordered pair of points in the same position space, with all coordinates having the same quantity dimension and unit (length an meters).[15][16] A sliding vector is the combination of an ordinary vector quantity and a line of application or line of action, over which the vector quantity can be translated (without rotations). A free vector is a vector quantity having an undefined support or region of application; it can be freely translated with no consequences; a displacement vector is a prototypical example of free vector.
Aside from the notion of units and support, physical vector quantities may also differ from Euclidean vectors in terms of metric. For example, an event in spacetime may be represented as a position four-vector, with coherent derived unit of meters: it includes a position Euclidean vector and a timelike component, t ⋅ c0 (involving the speed of light). In that case, the Minkowski metric is adopted instead of the Euclidean metric.
Vector quantities are a generalization of scalar quantities and can be further generalized as tensor quantities.[16] Individual vectors may be ordered in a sequence over time (a time series), such as position vectors discretizing a trajectory. A vector may also result from the evaluation, at a particular instant, of a continuous vector-valued function (e.g., the pendulum equation). In the natural sciences, the term "vector quantity" also encompasses vector fields defined over a two- or three-dimensional region of space, such as wind velocity over Earth's surface.
Pseudo vectors and bivectors are also admitted as physical vector quantities.Vector spaces
[edit]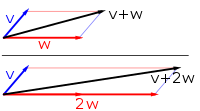
In mathematics and physics, a vector space (also called a linear space) is a set whose elements, often called vectors, can be added together and multiplied ("scaled") by numbers called scalars. The operations of vector addition and scalar multiplication must satisfy certain requirements, called vector axioms. Real vector spaces and complex vector spaces are kinds of vector spaces based on different kinds of scalars: real numbers and complex numbers. Scalars can also be, more generally, elements of any field.
Vector spaces generalize Euclidean vectors, which allow modeling of physical quantities (such as forces and velocity) that have not only a magnitude, but also a direction. The concept of vector spaces is fundamental for linear algebra, together with the concept of matrices, which allows computing in vector spaces. This provides a concise and synthetic way for manipulating and studying systems of linear equations.
Vector spaces are characterized by their dimension, which, roughly speaking, specifies the number of independent directions in the space. This means that, for two vector spaces over a given field and with the same dimension, the properties that depend only on the vector-space structure are exactly the same (technically the vector spaces are isomorphic). A vector space is finite-dimensional if its dimension is a natural number. Otherwise, it is infinite-dimensional, and its dimension is an infinite cardinal. Finite-dimensional vector spaces occur naturally in geometry and related areas. Infinite-dimensional vector spaces occur in many areas of mathematics. For example, polynomial rings are countably infinite-dimensional vector spaces, and many function spaces have the cardinality of the continuum as a dimension.
Many vector spaces that are considered in mathematics are also endowed with other structures. This is the case of algebras, which include field extensions, polynomial rings, associative algebras and Lie algebras. This is also the case of topological vector spaces, which include function spaces, inner product spaces, normed spaces, Hilbert spaces and Banach spaces.Vectors in algebra
[edit]Every algebra over a field is a vector space, but elements of an algebra are generally not called vectors. However, in some cases, they are called vectors, mainly due to historical reasons.
- Vector quaternion, a quaternion with a zero real part
- Multivector or p-vector, an element of the exterior algebra of a vector space.
- Spinors, also called spin vectors, have been introduced for extending the notion of rotation vector. In fact, rotation vectors represent well rotations locally, but not globally, because a closed loop in the space of rotation vectors may induce a curve in the space of rotations that is not a loop. Also, the manifold of rotation vectors is orientable, while the manifold of rotations is not. Spinors are elements of a vector subspace of some Clifford algebra.
- Witt vector, an infinite sequence of elements of a commutative ring, which belongs to an algebra over this ring, and has been introduced for handling carry propagation in the operations on p-adic numbers.
Data represented by vectors
[edit]This section's factual accuracy is disputed. (November 2021) |
The set of tuples of n real numbers has a natural structure of vector space defined by component-wise addition and scalar multiplication. It is common to call these tuples vectors, even in contexts where vector-space operations do not apply. More generally, when some data can be represented naturally by vectors, they are often called vectors even when addition and scalar multiplication of vectors are not valid operations on these data.[disputed – discuss] Here are some examples.
- Rotation vector, a Euclidean vector whose direction is that of the axis of a rotation and magnitude is the angle of the rotation.
- Burgers vector, a vector that represents the magnitude and direction of the lattice distortion of dislocation in a crystal lattice
- Interval vector, in musical set theory, an array that expresses the intervallic content of a pitch-class set
- Probability vector, in statistics, a vector with non-negative entries that sum to one.
- Random vector or multivariate random variable, in statistics, a set of real-valued random variables that may be correlated. However, a random vector may also refer to a random variable that takes its values in a vector space.
- Logical vector, a vector of 0s and 1s (Booleans).
Vectors in calculus
[edit]Calculus serves as a foundational mathematical tool in the realm of vectors, offering a framework for the analysis and manipulation of vector quantities in diverse scientific disciplines, notably physics and engineering. Vector-valued functions, where the output is a vector, are scrutinized using calculus to derive essential insights into motion within three-dimensional space. Vector calculus extends traditional calculus principles to vector fields, introducing operations like gradient, divergence, and curl, which find applications in physics and engineering contexts. Line integrals, crucial for calculating work along a path within force fields, and surface integrals, employed to determine quantities like flux, illustrate the practical utility of calculus in vector analysis. Volume integrals, essential for computations involving scalar or vector fields over three-dimensional regions, contribute to understanding mass distribution, charge density, and fluid flow rates.[citation needed]
See also
[edit]Vector spaces with more structure
[edit]- Graded vector space, a type of vector space that includes the extra structure of gradation
- Normed vector space, a vector space on which a norm is defined
- Hilbert space
- Ordered vector space, a vector space equipped with a partial order
- Super vector space, name for a Z2-graded vector space
- Symplectic vector space, a vector space V equipped with a non-degenerate, skew-symmetric, bilinear form
- Topological vector space, a blend of topological structure with the algebraic concept of a vector space
Vector fields
[edit]A vector field is a vector-valued function that, generally, has a domain of the same dimension (as a manifold) as its codomain,
- Conservative vector field, a vector field that is the gradient of a scalar potential field
- Hamiltonian vector field, a vector field defined for any energy function or Hamiltonian
- Killing vector field, a vector field on a Riemannian manifold associated with a symmetry
- Solenoidal vector field, a vector field with zero divergence
- Vector potential, a vector field whose curl is a given vector field
- Vector flow, a set of closely related concepts of the flow determined by a vector field
See also
[edit]- Ricci calculus
- Vector Analysis, a textbook on vector calculus by Wilson, first published in 1901, which did much to standardize the notation and vocabulary of three-dimensional linear algebra and vector calculus
- Vector bundle, a topological construction that makes precise the idea of a family of vector spaces parameterized by another space
- Vector calculus, a branch of mathematics concerned with differentiation and integration of vector fields
- Vector differential, or del, a vector differential operator represented by the nabla symbol
- Vector Laplacian, the vector Laplace operator, denoted by , is a differential operator defined over a vector field
- Vector notation, common notation used when working with vectors
- Vector operator, a type of differential operator used in vector calculus
- Vector product, or cross product, an operation on two vectors in a three-dimensional Euclidean space, producing a third three-dimensional Euclidean vector perpendicular to the original two
- Vector projection, also known as vector resolute or vector component, a linear mapping producing a vector parallel to a second vector
- Vector-valued function, a function that has a vector space as a codomain
- Vectorization (mathematics), a linear transformation that converts a matrix into a column vector
- Vector autoregression, an econometric model used to capture the evolution and the interdependencies between multiple time series
- Vector boson, a boson with the spin quantum number equal to 1
- Vector measure, a function defined on a family of sets and taking vector values satisfying certain properties
- Vector meson, a meson with total spin 1 and odd parity
- Vector quantization, a quantization technique used in signal processing
- Vector soliton, a solitary wave with multiple components coupled together that maintains its shape during propagation
- Vector synthesis, a type of audio synthesis
- Phase vector
Notes
[edit]- ^ Ivanov 2001
- ^ Heinbockel 2001
- ^ Itô 1993, p. 1678; Pedoe 1988
- ^ Latin: vectus, perfect participle of vehere, "to carry"/ veho = "I carry". For historical development of the word vector, see "vector n.". Oxford English Dictionary (Online ed.). Oxford University Press. (Subscription or participating institution membership required.) and Jeff Miller. "Earliest Known Uses of Some of the Words of Mathematics". Retrieved 2007-05-25.
- ^ The Oxford English Dictionary (2nd. ed.). London: Clarendon Press. 2001. ISBN 9780195219425.
- ^ "vector | Definition & Facts". Encyclopedia Britannica. Retrieved 2020-08-19.
- ^ "Vectors". www.mathsisfun.com. Retrieved 2020-08-19.
- ^ Weisstein, Eric W. "Vector". mathworld.wolfram.com. Retrieved 2020-08-19.
- ^ a b c "Details for IEV number 102-03-21: "vector quantity"". International Electrotechnical Vocabulary (in Japanese). Retrieved 2024-09-07.
- ^ "Details for IEV number 102-03-04: "vector"". International Electrotechnical Vocabulary (in Japanese). Retrieved 2024-09-07.
- ^ a b Rao, A. (2006). Dynamics of Particles and Rigid Bodies: A Systematic Approach. Cambridge University Press. p. 3. ISBN 978-0-521-85811-3. Retrieved 2024-09-08.
- ^ a b Teodorescu, Petre P. (2007-06-06). Mechanical Systems, Classical Models: Volume 1: Particle Mechanics. Springer Science & Business Media. ISBN 978-1-4020-5442-6.
- ^ Merches, I.; Radu, D. (2014). Analytical Mechanics: Solutions to Problems in Classical Physics. CRC Press. p. 379. ISBN 978-1-4822-3940-9. Retrieved 2024-09-09.
- ^ Borisenko, A.I.; Tarapov, I.E.; Silverman, R.A. (2012). Vector and Tensor Analysis with Applications. Dover Books on Mathematics. Dover Publications. p. 2. ISBN 978-0-486-13190-0. Retrieved 2024-09-08.
- ^ "Appendix A. Linear Algebra from a Geometric Point of View". Differential Geometry: A Geometric Introduction. Ithaca, NY: David W. Henderson. 2013. pp. 121–138. doi:10.3792/euclid/9781429799843-13. ISBN 978-1-4297-9984-3.
- ^ a b "ISO 80000-2:2019 - Quantities and units - Part 2: Mathematics". ISO. 2013-08-20. Retrieved 2024-09-08.
References
[edit]- Vectors - The Feynman Lectures on Physics
- Heinbockel, J. H. (2001). Introduction to Tensor Calculus and Continuum Mechanics. Trafford Publishing. ISBN 1-55369-133-4.
- Itô, Kiyosi (1993). Encyclopedic Dictionary of Mathematics (2nd ed.). MIT Press. ISBN 978-0-262-59020-4.
- Ivanov, A.B. (2001) [1994], "Vector", Encyclopedia of Mathematics, EMS Press
- Pedoe, Daniel (1988). Geometry: A comprehensive course. Dover. ISBN 0-486-65812-0.




